题目内容
已知命题:
①“偶函数的图象关于y轴对称”的逆命题;
②三个实数a,b,c成等比数列的充要条件是b2=ac;
③“?x∈R,x2-x+1>0”;
④存在不共线的向量
,
,使得
=k
k∈R成立.其中真命题是( )
①“偶函数的图象关于y轴对称”的逆命题;
②三个实数a,b,c成等比数列的充要条件是b2=ac;
③“?x∈R,x2-x+1>0”;
④存在不共线的向量
| a |
| b |
| a |
| b |
| A、①②③ | B、①④ | C、②③ | D、①③ |
分析:对于①,先写出它的逆命题然后再判断;对于②,考虑特殊情形:其中一个为0时进行判断;对于③,利用根的判别式解决;对于④,利用共线向量的基本定理即可解决.
解答:解:对于①,“偶函数的图象关于y轴对称”的逆命题是:“函数的图象关于y轴对称则此函数是偶函数”,它是真命题;
对于②,三个实数a,b,c成等比数列可得出b2=ac;但是,反之不成立(如其中一个为0时),故错;
对于③,由于x2-x+1的判别式△<0,故x2-x+1>0恒成立,它是真命题;
对于④,不存在不共线的向量
,
,使得
=k
k∈R成立,故它是假命题.
故只有①③是真命题.
故选D.
对于②,三个实数a,b,c成等比数列可得出b2=ac;但是,反之不成立(如其中一个为0时),故错;
对于③,由于x2-x+1的判别式△<0,故x2-x+1>0恒成立,它是真命题;
对于④,不存在不共线的向量
| a |
| b |
| a |
| b |
故只有①③是真命题.
故选D.
点评:本题主要考查了四种命题间的逆否关系、必要条件、充分条件与充要条件的判断,以及向量的共线定理,属于基础题.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
 是偶函数;命题q:?a∈R,g(x)=ax2+2x-1在(0,+∞)上单调递减,则下列结论正确的是
是偶函数;命题q:?a∈R,g(x)=ax2+2x-1在(0,+∞)上单调递减,则下列结论正确的是 ,使得
,使得 成立.其中真命题是
成立.其中真命题是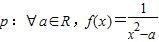 是偶函数;命题q:?a∈R,g(x)=ax2+2x-1在(0,+∞)上单调递减,则下列结论正确的是( )
是偶函数;命题q:?a∈R,g(x)=ax2+2x-1在(0,+∞)上单调递减,则下列结论正确的是( )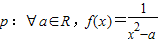 是偶函数;命题q:?a∈R,g(x)=ax2+2x-1在(0,+∞)上单调递减,则下列结论正确的是( )
是偶函数;命题q:?a∈R,g(x)=ax2+2x-1在(0,+∞)上单调递减,则下列结论正确的是( )