题目内容
四面体ABCD中,设M是CD的中点,则 化简的结果是( )
化简的结果是( )
A.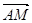 | B. | C. | D.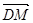 |
A
解析试题分析:根据题意,∵四面体ABCD中,M是CD的中点,故可知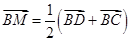 ,那么由于
,那么由于 ,故选A。
,故选A。
考点:向量加法及其几何意义
点评:本题考查的知识点是向量加法及其几何意义,其中根据M是CD的中点,得到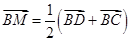 )是解答本题的关键.
)是解答本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知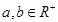 ,若向量
,若向量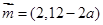 与向量
与向量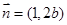 共线,则
共线,则 的最大值为( )
的最大值为( )
| A.6 | B.4 | C.3 | D. |
如图,平行四边形ABCD中,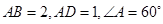 ,点M在AB边上,且
,点M在AB边上,且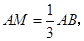 则
则 等于 ( )
等于 ( )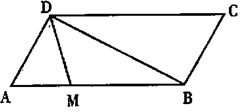
A.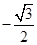 | B. | C.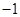 | D.1 |
已知 是平面向量,下列命题中真命题的个数是( )
是平面向量,下列命题中真命题的个数是( )
①  ②
② 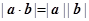
③  ④
④ 
| A.1 | B.2 | C.3 | D.4 |
设 是两个非零向量,下列选项正确的是( )
是两个非零向量,下列选项正确的是( )
A.若 ,则 ,则 |
B.若 ,则 ,则 |
C.若 ,则存在实数 ,则存在实数 ,使得 ,使得 |
D.若存在实数 ,使得 ,使得 ,则 ,则 |
如图,在边长为2的菱形ABCD中,∠BAD
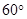 ,
,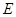 为
为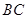 的中点,则
的中点,则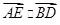

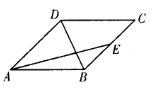
A.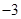 | B.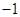 | C. | D. |
设 ,
, ,
,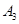 ,
, 是平面直角坐标系中两两不同的四点,若
是平面直角坐标系中两两不同的四点,若 ,
, ,且
,且 ,则称
,则称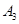 ,
, 调和分割
调和分割 ,
, ,已知点C(c,0),
,已知点C(c,0),
D(d,0) (c,d∈R)调和分割点A(0,0),B(1,0),则下面说法正确的是( )
| A.C可能是线段AB的中点 | B.D可能是线段AB的中点 |
| C.C,D可能同时在线段AB上 | D.C,D不可能同时在线段AB的延长线上 |
已知 和点M满足
和点M满足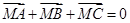 .若存在实
.若存在实 使得
使得 成立,则
成立,则 =( )
=( )
| A.2 | B.3 | C.4 | D.5 |
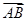 与
与 是两平行向量
是两平行向量 ,则A、B、C、D四点构成平行四边形
,则A、B、C、D四点构成平行四边形