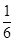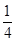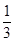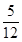题目内容
2014年西安地区特长生考试有8所名校招生,若某3位同学恰好被其中的2 所名校录取,则不同的录取方法有
| A.68种 | B.84种 | C.168种 | D.224种 |
C
解析试题分析:可以从反面考虑得: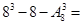 168.
168.
考点:排列组合问题.

练习册系列答案
相关题目
设已知 均为整数(
均为整数( ),若
),若 和
和 被
被 除所得的余数相同,则称
除所得的余数相同,则称 和
和 对模
对模 同余,记为
同余,记为  ,若
,若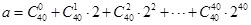 ,且
,且 , 则
, 则 的值可以是( )
的值可以是( )
| A.2011 | B.2012 | C.2013 | D.2014 |
在高校自主招生中,某学校获得5个推荐名额,其中清华大学2名,北京大学2名,复旦大学1名。并且北京大学和清华大学都要求必须有男生参加。学校通过选拔定下3男2女共5个推荐对象,则不同的推荐方法共有( )
| A.20种 | B.22种 | C.24种 | D.36种 |
若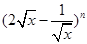 展开式中所有项的二项式系数之和为64,则展开式中含
展开式中所有项的二项式系数之和为64,则展开式中含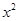 项的系数是( )
项的系数是( )
| A.192 | B.182 | C.-192 | D.-182 |
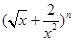 展开式中只有第六项二项式系数最大,则展开式中的常数项是( )
展开式中只有第六项二项式系数最大,则展开式中的常数项是( )
| A.180 | B.90 | C.45 | D.360 |
 展开式中的常数项为( )
展开式中的常数项为( )
A.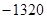 | B.1320 | C.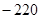 | D.220 |
已知(x-m)7=a0+a1x+a2x2+…+a7x7的展开式中x5的系数是189,则实数m=( )
| A.3 | B.-3 | C.±3 | D.5 |
若(3x+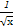 )n的展开式中各项系数的和为1024,则展开式中含x的整数次幂的项共有( )
)n的展开式中各项系数的和为1024,则展开式中含x的整数次幂的项共有( )
| A.2项 | B.3项 | C.5项 | D.6项 |
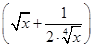 n的展开式中,前三项的系数成等差数列,把展开式中所有的项重新排成一列,有理项都互不相邻的概率为( )
n的展开式中,前三项的系数成等差数列,把展开式中所有的项重新排成一列,有理项都互不相邻的概率为( )