题目内容
一位国王的铸币大臣在每箱100枚的硬币中各掺入了一枚劣币,国王怀疑大臣作弊,他用两种方法来检测.方法一:在10箱中各任意抽查一枚;方法二:在5箱中各任意抽查两枚.国王用方法一、二能发现至少一枚劣币的概率分别记为P1和P2.则( )
| A、P1=P2 | B、P1<P2 | C、P1>P2 | D、以上三种情况都有可能 |
分析:每箱中抽到劣币的可能性都相等,故可用独立重复试验求解,又因为事件“发现至少一枚劣币”的对立事件是“没有劣币”,概率好求.方法一概率为1-0.9910;方法二概率为1-(
)5,做差比较大小即可.
| 49 |
| 50 |
解答:解:方案一:此方案下,每箱中的劣币被选中的概率为
,没有发现劣币的概率是0.99,故至少发现一枚劣币的总概率为1-0.9910;
方案二:此方案下,每箱的劣币被选中的概率为
,总事件的概率为1-(
)5,
作差得P1-P2=(
)5-0.9910,由计算器算得P1-P2<0
∴P1<P2.
故选B
| 1 |
| 100 |
方案二:此方案下,每箱的劣币被选中的概率为
| 1 |
| 50 |
| 49 |
| 50 |
作差得P1-P2=(
| 49 |
| 50 |
∴P1<P2.
故选B
点评:本题考查独立重复试验的概率和对立事件的概率问题,以及利用概率知识解决问题的能力.

练习册系列答案
相关题目
 和
和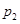 ,则(
)
,则(
) =
=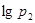 B、
B、 和
和 ,则( )
,则( )