题目内容
甲和乙参加智力答题活动,活动规则:①答题过程中,若答对则继续答题;若答错则停止答题;②每人最多答3个题;③答对第一题得10分,第二题得20分,第三题得30分,答错得0分.已知甲答对每个题的概率为| 3 |
| 4 |
| 1 |
| 3 |
(Ⅰ)求甲恰好得30分的概率;
(Ⅱ)设乙的得分为ξ,求ξ的分布列和数学期望;
(Ⅲ)求甲恰好比乙多30分的概率.
分析:(1)要求甲恰好得30分的概率,我们分析活动规则后可得,甲恰好得30分,说明甲前两题都答对,而第三题答错,代入分步事件概率公式即可得到答案.
(2)设乙的得分为ξ,则ξ的取值为0,10,30,60,我们根据活动规则,分析出ξ取不同值时的情况,代入概率公式即可求解.(3)要求甲恰好比乙多30分的概率,我们要先分析甲恰好比乙多30分的发生情况,由(2)的结论,共有两种情况,即甲恰好得30分且乙恰好得0分,或是甲恰好得60分且乙恰好得30分,代入概率公式即可求解.
(2)设乙的得分为ξ,则ξ的取值为0,10,30,60,我们根据活动规则,分析出ξ取不同值时的情况,代入概率公式即可求解.(3)要求甲恰好比乙多30分的概率,我们要先分析甲恰好比乙多30分的发生情况,由(2)的结论,共有两种情况,即甲恰好得30分且乙恰好得0分,或是甲恰好得60分且乙恰好得30分,代入概率公式即可求解.
解答:解:(I)甲恰好得30分,说明甲前两题都答对,而第三题答错,
其概率为(
)2(1-
)=
(II)ξ的取值为0,10,30,60
P(ξ=0)=1-
=
,
P(ξ=10)=(1-
)•(
)=
,
P(ξ=30)=
•
•(1-
)=
,
P(ξ=60)=(
)3=
ξ的概率分布如下表:
 E(ξ)=0×
E(ξ)=0×
+10×
+30×
+60×
=
(III)设甲恰好比乙多30分为事件A,
甲恰好得30分且乙恰好得0分为事件B1,
甲恰好得60分且乙恰好得30分为事件B2,
则A=B1∪B2,B1,B2为互斥事件.
P(A)=P(B1)+P(B2)=(
)2•
•
+(
)3•
=
.
所以,甲恰好比乙多30分的概率为
其概率为(
| 3 |
| 4 |
| 3 |
| 4 |
| 9 |
| 64 |
(II)ξ的取值为0,10,30,60
P(ξ=0)=1-
| 1 |
| 3 |
| 2 |
| 3 |
P(ξ=10)=(1-
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 9 |
P(ξ=30)=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 27 |
P(ξ=60)=(
| 1 |
| 3 |
| 1 |
| 27 |
ξ的概率分布如下表:
 E(ξ)=0×
E(ξ)=0×| 2 |
| 3 |
| 2 |
| 9 |
| 2 |
| 27 |
| 1 |
| 27 |
| 20 |
| 3 |
(III)设甲恰好比乙多30分为事件A,
甲恰好得30分且乙恰好得0分为事件B1,
甲恰好得60分且乙恰好得30分为事件B2,
则A=B1∪B2,B1,B2为互斥事件.
P(A)=P(B1)+P(B2)=(
| 3 |
| 4 |
| 1 |
| 4 |
| 2 |
| 3 |
| 3 |
| 4 |
| 2 |
| 27 |
| 1 |
| 8 |
所以,甲恰好比乙多30分的概率为
| 1 |
| 8 |
点评:本小题主要考查相互独立事件概率的计算,运用数学知识解决问题的能力,要想计算一个事件的概率,首先我们要分析这个事件是分类的(分几类)还是分步的(分几步),然后再利用加法原理和乘法原理进行求解.

练习册系列答案
相关题目
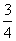 ,乙答对每个题的概率为
,乙答对每个题的概率为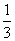 。
。 ,求
,求 ,乙答对每个题的概率为
,乙答对每个题的概率为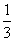 。
。 ,求
,求 ,乙答对每个题的概率为
,乙答对每个题的概率为 .
.