题目内容
对于定义在实数集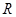 上的两个函数
上的两个函数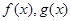 ,若存在一次函数
,若存在一次函数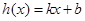 使得,对任意的
使得,对任意的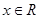 ,都有
,都有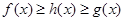 ,则把函数
,则把函数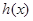 的图像叫函数
的图像叫函数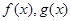 的“分界线”。现已知
的“分界线”。现已知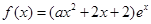 (
(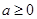 ,
,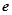 为自然对数的底数),
为自然对数的底数),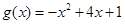
(1)求 的递增区间;
的递增区间;
(2)当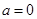 时,函数
时,函数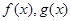 是否存在过点
是否存在过点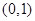 的“分界线”?若存在,求出函数
的“分界线”?若存在,求出函数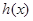 的解析式,若不存在,请说明理由。
的解析式,若不存在,请说明理由。
【答案】
(1)若 递增区间为
递增区间为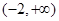 ,若
,若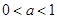 递增区间为
递增区间为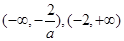 ,若
,若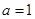 ,则递增区间为
,则递增区间为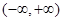 若
若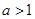 递增区间为
递增区间为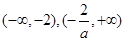 (2)存在函数
(2)存在函数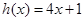 的图像是函数
的图像是函数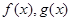 过点
过点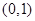 的“分界线”。
的“分界线”。
【解析】
试题分析:(1)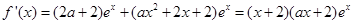 ,
,
由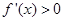 得
得
①若 ,则
,则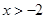 ,此时
,此时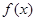 的递增区间为
的递增区间为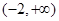 ;
;
②若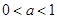 ,则
,则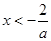 或
或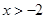 ,此时
,此时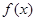 的递增区间为
的递增区间为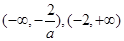 ;
;
③若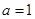 ,则
,则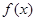 的递增区间为
的递增区间为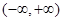 ;
;
④若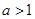 ,则
,则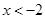 或
或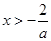 ,此时
,此时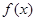 的递增区间为
的递增区间为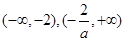 。
。
(2)当 时,
时,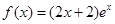 ,假设存在实数
,假设存在实数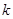 ,使不等式
,使不等式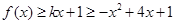 对
对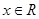 恒成立,
恒成立,
由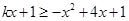 得到
得到 对
对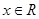 恒成立,
恒成立,
则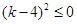 ,得
,得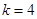 ,
,
下面证明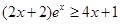 对
对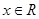 恒成立。
恒成立。
设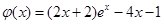 ,
, ,
,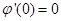 ,
,
且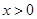 时,
时,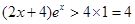 ,
,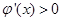 ,
,
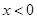 时,
时, ,
,
所以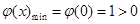 ,即
,即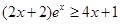 对
对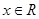 恒成立。
恒成立。
综上,存在函数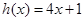 的图像是函数
的图像是函数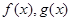 过点
过点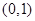 的“分界线”。
的“分界线”。
考点:函数单调区间及不等式恒成立
点评:第一小题求单调区间针对于不同的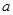 值对应不同的极值点,因此需对
值对应不同的极值点,因此需对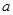 值分情况讨论以求单调性;第二问在正确理解给定信息的基础上将问题转化为不等式恒成立问题,进而转化为函数最值,可利用导数这一工具求解
值分情况讨论以求单调性;第二问在正确理解给定信息的基础上将问题转化为不等式恒成立问题,进而转化为函数最值,可利用导数这一工具求解

练习册系列答案
相关题目
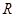 上的两个函数
上的两个函数 ,若存在一次函数
,若存在一次函数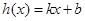 使得,对任意的
使得,对任意的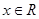 ,都有
,都有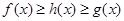 ,则把函数
,则把函数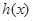 的图像叫函数
的图像叫函数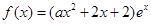 (
(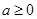 ,
,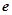 为自然对数的底数),
为自然对数的底数),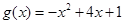
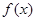 的递增区间;
的递增区间;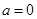 时,函数
时,函数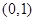 的“分界线”?若存在,求出函数
的“分界线”?若存在,求出函数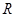 上的函数
上的函数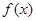 图像连续不断,且
图像连续不断,且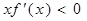 ,则必有(
)
,则必有(
) B.
B.
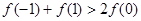
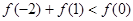 D.
D.
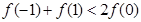
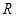 上的函数
上的函数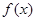 图像连续不断,且
图像连续不断,且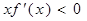 ,则必有(
)
,则必有(
)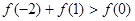 B.
B.
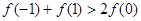
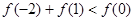 D.
D.
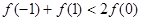
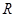 上的函数
上的函数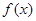 ,若
,若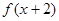 都是偶函数,则( )
都是偶函数,则( ) 为偶函数
B.
为偶函数
B.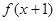 为奇函数
为奇函数
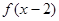 为偶函数
D.
为偶函数
D.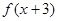 为奇函数
为奇函数