题目内容
在空间坐标系中,已知直角三角形ABC的三个顶点为A(-3,-2,1)、B(-1,-1,-1)、C(-5,x,0),则x的值为
0或9
0或9
.分析:先利用坐标,求出向量,再分类讨论,利用数量积为0,即可求得x的值.
解答:解:∵A(-3,-2,1)、B(-1,-1,-1)、C(-5,x,0),
∴
=(2,1,-2),
=(-4,x+1,1),
=(-2,x+2,-1)
分三种情况:
①A为直角,
•
=0,∴-4+x+2+2=0,∴x=0
②B为直角,
•
=0,∴-8+x+1-2=0,∴x=9
③C为直角,
•
=0,∴8+(x+1)(x+2)-1=0,x2+3x+9=0,方程无解
综上,x的值为0或9
故答案为:0或9
∴
| AB |
| BC |
| AC |
分三种情况:
①A为直角,
| AB |
| AC |
②B为直角,
| AB |
| BC |
③C为直角,
| AC |
| BC |
综上,x的值为0或9
故答案为:0或9
点评:本题考查空间向量,考查分类讨论的数学思想,解题的关键是用坐标表示向量,利用数量积为0建立方程.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
 的三个顶点为A
的三个顶点为A 、B
、B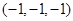 、C
、C ,则
,则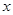 的值为 .
的值为 . 、B
、B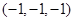 、C
、C ,则
,则 的值为 .
的值为 .