题目内容
若下列方程:x +4ax-4a+3=0, x
+4ax-4a+3=0, x +(a-1)x+a
+(a-1)x+a =0, x
=0, x +2ax-2a=0至少有一个方程有实根。试求实数a的取值范围。
+2ax-2a=0至少有一个方程有实根。试求实数a的取值范围。
 +4ax-4a+3=0, x
+4ax-4a+3=0, x +(a-1)x+a
+(a-1)x+a =0, x
=0, x +2ax-2a=0至少有一个方程有实根。试求实数a的取值范围。
+2ax-2a=0至少有一个方程有实根。试求实数a的取值范围。a≥-1或a≤-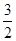
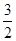
三个方程至少有一个方程有实根的反面情况仅有一种:三个方程均没有实根。先求出反面情况时a的范围,再所得范围的补集就是正面情况的答案。
解:设三个方程均无实根,则有:
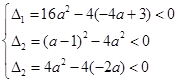 ,解得
,解得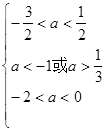 ,即-
,即-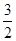 <a<-1。
<a<-1。
所以当a≥-1或a≤-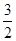 时,三个方程至少有一个方程有实根。
时,三个方程至少有一个方程有实根。
解:设三个方程均无实根,则有:
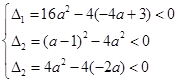 ,解得
,解得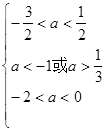 ,即-
,即-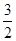 <a<-1。
<a<-1。所以当a≥-1或a≤-
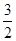 时,三个方程至少有一个方程有实根。
时,三个方程至少有一个方程有实根。
练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
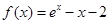 ,则函数
,则函数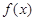 的零点所在区间为( )
的零点所在区间为( )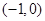
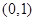
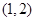
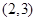
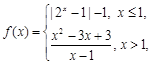 函数
函数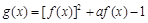 (其中a为常数),给出下列结论:
(其中a为常数),给出下列结论: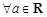 ,函数
,函数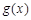 至少有一个零点;
至少有一个零点;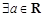 ,函数
,函数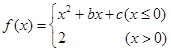 ,若
,若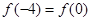 ,
,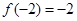 ,则关于
,则关于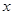 的方程
的方程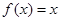 的解的个数为 ( )
的解的个数为 ( )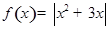 ,
,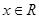 .若方程
.若方程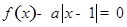 恰有4个互异的实数根,则实数
恰有4个互异的实数根,则实数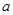 的取值范围为__________.
的取值范围为__________.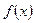 的图象经过点
的图象经过点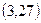 ,则
,则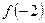 的值等于
的值等于