题目内容
(本题16分)
如图,F是抛物线![]() 的焦点,Q是准线与
的焦点,Q是准线与![]() 轴的交点,斜率为
轴的交点,斜率为![]() 的直线
的直线![]() 经过点Q.
经过点Q.
(1)当K取不同数值时,求直线![]() 与抛物线交点的个数;
与抛物线交点的个数;
(2)如直线![]() 与抛物线相交于A、B两点,求证:
与抛物线相交于A、B两点,求证:![]() 是定值
是定值
(3)在![]() 轴上是否存在这样的定点M,对任意的过点Q的直线
轴上是否存在这样的定点M,对任意的过点Q的直线![]() ,如
,如![]() 与抛物线相交于A、B两点,均能使得
与抛物线相交于A、B两点,均能使得![]() 为定值,有则找出满足条
为定值,有则找出满足条
件的点M;没有,则说明理由.
(1)△>0,即![]() 两个交点
两个交点
△=0,![]() 时一个交点
时一个交点
△<0,![]() 或
或![]() 无交点
无交点
解析:
(1)设![]() 代入
代入![]()
得:![]() (*)
(*)
![]()
![]() ,一个交点(1’)
,一个交点(1’)
![]()
![]() ,△
,△![]() ,
,
△>0,即![]() 两个交点(3’)
两个交点(3’)
△=0,![]() 时一个交点(4’)
时一个交点(4’)
△<0,![]() 或
或![]() 无交点(5’)
无交点(5’)
(2)设交点![]() ,
,![]()
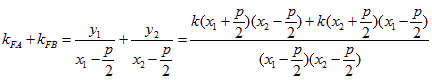 (8’)
(8’)
 斜率和为定值0(10’)
斜率和为定值0(10’)
(3)如存在满足条件的点M![]() ,使得
,使得![]() 为定值
为定值

 (14’)
(14’)
仅当![]() ,即
,即![]() 时,
时,![]() (16’)
(16’)

练习册系列答案
相关题目
 面山顶上一座铁塔,塔高AB=80米,塔所在山高OA=220米,OC=200米,观测者所在斜坡CD近似看成直线,斜坡与水平面夹角为
面山顶上一座铁塔,塔高AB=80米,塔所在山高OA=220米,OC=200米,观测者所在斜坡CD近似看成直线,斜坡与水平面夹角为 ,
,
 轴的正向,OB为
轴的正向,OB为 轴正向,建立直角坐标系,求
轴正向,建立直角坐标系,求 出斜坡CD所在直线方程;
出斜坡CD所在直线方程;
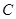 城周边已有两条公路
城周边已有两条公路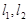 在点O处交汇,且它们的夹角为
在点O处交汇,且它们的夹角为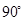 .已知
.已知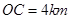 ,
, 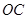 与公路
与公路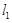 夹角为
夹角为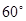 .现规划在公路
.现规划在公路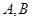 两处作为交汇点(异于点O)直接修建一条公路通过
两处作为交汇点(异于点O)直接修建一条公路通过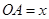
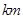 ,
,
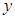 关于
关于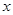 的函数关系式并指出它的定义域;
的函数关系式并指出它的定义域;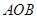 的面积最小.
的面积最小.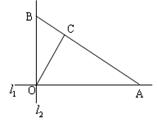
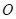 离地面1米,风车圆周上一点A从最底点
离地面1米,风车圆周上一点A从最底点
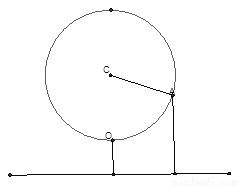
 的焦点,Q是准线与
的焦点,Q是准线与 轴的交点,斜率为
轴的交点,斜率为 的直线
的直线 经过点Q.
经过点Q. 是定值
是定值 为定值,有则找出满足条
为定值,有则找出满足条