题目内容
函数fM(x)的定义域为R,且定义如下:fM(x)=
|
| fA∪B(x)+1 |
| fA(x)+fB(x)+1 |
分析:对F(x)中的x属于什么集合进行分类讨论,利用题中新定义的函数求出f(x)的函数值,从而得到F(x)的值域即可.
解答:解:当x∈CR(A∪B)时,f(A∪B)(x)=0,fA(x)=0,
fB(x)=0,
∴F(x)=
=1,
同理得:当x∈B时,F(x)=1;
当x∈A时,F(x)=1;故:
F(x)=
,值域为{1}.
故答案为:{1}.
fB(x)=0,
∴F(x)=
| 0+1 |
| 0+0+1 |
同理得:当x∈B时,F(x)=1;
当x∈A时,F(x)=1;故:
F(x)=
|
故答案为:{1}.
点评:本题主要考查了函数的值域、分段函数,属于创新型题目.

练习册系列答案
相关题目
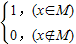 (其中M为非空数集且M?R),在实数集R上有两个非空真子集A、B满足A∩B≡∅,则函数F(x)=
(其中M为非空数集且M?R),在实数集R上有两个非空真子集A、B满足A∩B≡∅,则函数F(x)=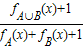 的值域为( )
的值域为( )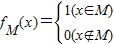 (其中M为非空数集且M?R),在实数集R上有两个非空真子集A、B满足A∩B=∅,则函数
(其中M为非空数集且M?R),在实数集R上有两个非空真子集A、B满足A∩B=∅,则函数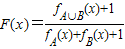 的值域为 .
的值域为 .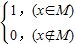 (其中M为非空数集且M?R),在实数集R上有两个非空真子集A、B满足A∩B≡∅,则函数F(x)=
(其中M为非空数集且M?R),在实数集R上有两个非空真子集A、B满足A∩B≡∅,则函数F(x)=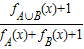 的值域为( )
的值域为( )