题目内容
(本题满分12分)
已知向量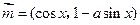 ,
,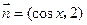 ,其中
,其中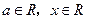 ,设
,设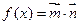 ,且函数
,且函数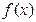 的最大值为
的最大值为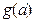 .。
.。
(Ⅰ)求函数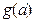 的解析式。
的解析式。
(Ⅱ)设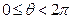 ,求函数
,求函数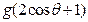 的最大值和最小值以及对应的
的最大值和最小值以及对应的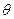 值。
值。
已知向量
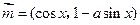 ,
,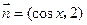 ,其中
,其中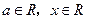 ,设
,设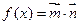 ,且函数
,且函数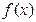 的最大值为
的最大值为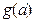 .。
.。(Ⅰ)求函数
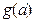 的解析式。
的解析式。(Ⅱ)设
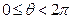 ,求函数
,求函数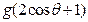 的最大值和最小值以及对应的
的最大值和最小值以及对应的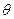 值。
值。(1)

(2)
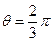
解:(Ⅰ)由题意知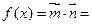
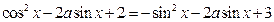 ,
,
令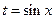 ,则
,则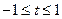 ,从而
,从而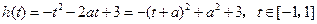 ,
,
对称轴为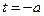 . --------------3分
. --------------3分
①当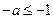 ,即
,即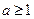 时,
时,
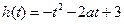 在
在 上单调递减,
上单调递减,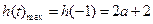 ;
;  ---5分
---5分
②当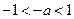 ,即
,即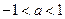 时
时 ,
,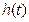 在
在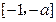 上单调递增,在
上单调递增,在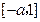 上单调递减∴
上单调递减∴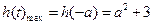 ; --------------7分
; --------------7分
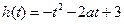 在
在 上单调递增,
上单调递增,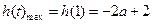 ;
;
综上, --------------8分
--------------8分
(2)由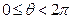 知,
知,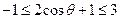 .又因为
.又因为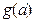 在
在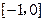 上单调递减,在
上单调递减,在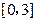 上单调递增,所以
上单调递增,所以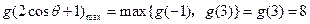 ,
,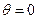 ;
;
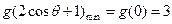 ,
,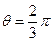 . --------------12分
. --------------12分
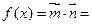
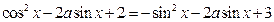 ,
, 令
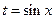 ,则
,则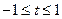 ,从而
,从而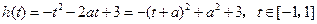 ,
,对称轴为
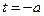 . --------------3分
. --------------3分①当
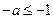 ,即
,即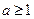 时,
时,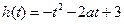 在
在 上单调递减,
上单调递减,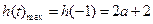 ;
;  ---5分
---5分②当
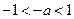 ,即
,即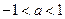 时
时 ,
,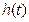 在
在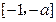 上单调递增,在
上单调递增,在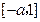 上单调递减∴
上单调递减∴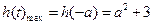 ; --------------7分
; --------------7分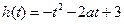 在
在 上单调递增,
上单调递增,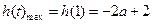 ;
;综上,
 --------------8分
--------------8分(2)由
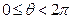 知,
知,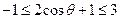 .又因为
.又因为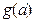 在
在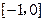 上单调递减,在
上单调递减,在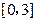 上单调递增,所以
上单调递增,所以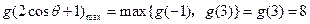 ,
,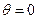 ;
;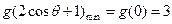 ,
,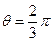 . --------------12分
. --------------12分
练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
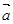 ︱=1,︱
︱=1,︱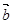 ︱=2,且
︱=2,且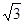
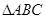 中,若
中,若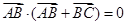 ,则
,则 的部分图象如图所示,则
的部分图象如图所示,则

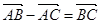 ②
②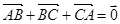 ③
③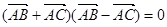 则?ABC是等腰三角形④若sin(A-
则?ABC是等腰三角形④若sin(A-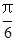 )=
)=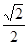 ,则角A=
,则角A=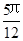 。其中正确的结论是
。其中正确的结论是 与
与 的夹角为
的夹角为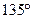 ,则
,则 的充要条件是
的充要条件是




 ,且
,且 ,则
,则 ( )
( )


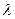 b,且|c|
b,且|c|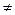 1,a
1,a (b-c)=0,则实数
(b-c)=0,则实数 、
、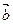 满足
满足 ,
, ,
, ,则
,则