题目内容
解答题
已知椭圆的长轴长是2
，焦点坐标分别为(－
，0)和(，0)．
(1)求这个椭圆的标准方程；
(2)如果直线y＝x＋m与这个椭圆相交于A、B两点，求|AB|的最大值．
答案：
解析：
解析：
|
(1)由题可知a＝ ∴椭圆标准方程为 (2)由 ∵直线与椭圆交于两点， ∴Δ＞0，即36m2－48(m2－1)＞0，解得－2＜m＜2． 由韦达定理得x1＋x2＝－ ∴|AB|＝ ∴当m＝0时，|AB|有最大值为 |
，c＝
，∴b＝1，
＋
＝1．
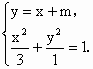消去y得4x2＋6mx＋3(m2－1)＝0．
m，x1x2＝
．
·|x1－x2|＝
·
＝
·
．
．
练习册系列答案
相关题目
、
是椭圆的两个焦点，P为椭圆上一点，且∠
，|BC|＝2|AC|．
．