题目内容
设函数f(x)=x2+2(-2≤x<0),其反函数为f-1(x),则f-1(3)= ( )
| A.-1 | B.1 | C.0或1 | D.1或-1 |
A
解析

练习册系列答案
相关题目
若函数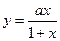 的图像关于直线
的图像关于直线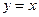 对称,则
对称,则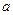 为
为
A.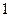 | B.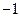 | C.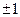 | D.任意实数 |
设f(x)为定义在R上的奇函数,当x≥0时,f(x)=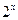 +2x+b(b为常数),则f(-1)=
+2x+b(b为常数),则f(-1)=
| A.3 | B.1 | C.-1 | D.-3 |
设函数 ,则
,则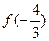 的值为( )
的值为( )
A.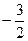 | B.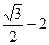 | C.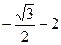 | D.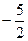 |
已知函数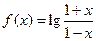 ,实数
,实数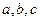 满足
满足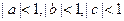 ,且
,且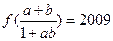 ,
,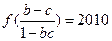 ,则
,则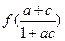 的值
的值
| A.-1 | B.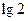 | C.1 | D.3 |
若函数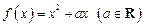 ,则下列结论正确的是( )
,则下列结论正确的是( )
A.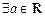 , , 是偶函数 是偶函数 |
B.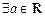 , , 是奇函数 是奇函数 |
C.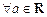 , , 在(0,+∞)上是增函数 在(0,+∞)上是增函数 |
D.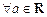 , , 在(0,+∞)上是减函数 在(0,+∞)上是减函数 |
已知函数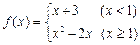 ,若
,若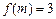 ,则m的值为 ( )
,则m的值为 ( )
| A.0或3 | B.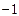 或3 或3 | C.0或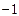 | D.0 |
 在定义域
在定义域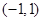 上是减函数,且
上是减函数,且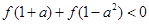 ,则实数
,则实数 的取值范围是__________.
的取值范围是__________.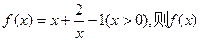 ( )
( )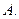 有最小值
有最小值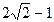
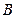 .有最大值
.有最大值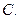 有最大值
有最大值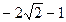
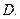 有最大值
有最大值