题目内容
我校为了了解高二级学生参加体育活动的情况,随机抽取了100名高二级学生进行调查.下面是根据调查结果绘制的学生日均参加体育活动时间的频率分布直方图:
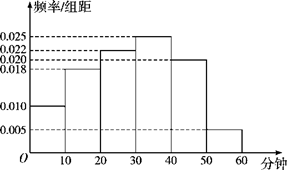
将日均参加体育活动时间不低于40分钟的学生称为参加体育活动的“积极分子”.根据已知条件完成下面的列联表,并据此资料,在犯错误的概率不超过5%的前提下,你是否认为参加体育活动的“积极分子”与性别有关?

将日均参加体育活动时间不低于40分钟的学生称为参加体育活动的“积极分子”.根据已知条件完成下面的列联表,并据此资料,在犯错误的概率不超过5%的前提下,你是否认为参加体育活动的“积极分子”与性别有关?
| | 非积极分子 | 积极分子 | 合计 |
| 男 | | 15 | 45 |
| 女 | | | |
| 合计 | | | |
| | 非积极分子 | 积极分子 | 合计 |
| 男 | 30 | 15 | 45 |
| 女 | 45 | 10 | 55 |
| 合计 | 75 | 25 | 100 |
没有理由认为“积极分子”与性别有关.
试题分析:根据图中所给的频率分布直方图可知在抽取的100人中,“积极分子”有25人,因此列联表易得,通过计算K2=
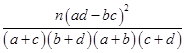 =
= =
=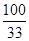 ≈3.030,可得没有理由认为“积极分子”与性别有关.
≈3.030,可得没有理由认为“积极分子”与性别有关.由频率分布直方图可知,在抽取的100人中,“积极分子”有25人,
从而2×2列联表如下:
| | 非积极分子 | 积极分子 | 合计 |
| 男 | 30 | 15 | 45 |
| 女 | 45 | 10 | 55 |
| 合计 | 75 | 25 | 100 |
由2×2列联表中数据代入公式计算,得:
K2=
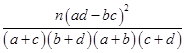 =
= =
=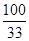 ≈3.030. 11分
≈3.030. 11分因为3.030<3.841,
所以,在犯错误的概率不超过5%的前提下, 没有理由认为“积极分子”与性别有关. 14分

练习册系列答案
相关题目
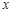 (万元)与销售额
(万元)与销售额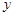 (万元)之间有如下的对应数据:
(万元)之间有如下的对应数据: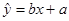 ,其中
,其中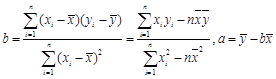 .
.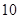 天空气质量指数(
天空气质量指数(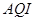 )和“
)和“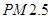 ”(直径小于等于
”(直径小于等于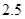 微米的颗粒物)
微米的颗粒物)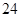 小时平均浓度的数据,空气质量指数(
小时平均浓度的数据,空气质量指数(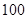 表示空气质量优良.
表示空气质量优良.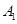
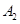
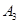
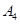
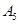
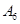
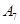
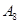
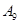
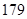
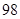
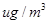 )
)

 为“抽取的两个日期中,当天‘
为“抽取的两个日期中,当天‘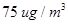 ”,求事件
”,求事件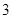 天,记
天,记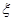 为“
为“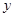 (单位:
(单位: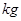 )与身高
)与身高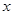 (单位:
(单位: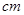 )具有线性相关关系,根据一组样本数据
)具有线性相关关系,根据一组样本数据 ,用最小二乘法建立的回归方程为
,用最小二乘法建立的回归方程为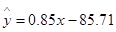 ,则下列结论中不正确的是( )
,则下列结论中不正确的是( )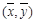
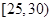 ,第2组
,第2组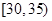 ,第3组
,第3组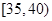 ,第4组
,第4组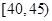 ,第5组
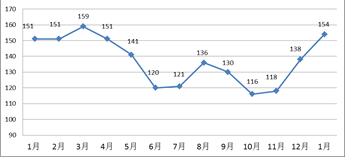
,第5组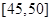 ,由统计的数据得到的频率分布直方图如图所示,在其右面的表是年龄的频率分布表。
,由统计的数据得到的频率分布直方图如图所示,在其右面的表是年龄的频率分布表。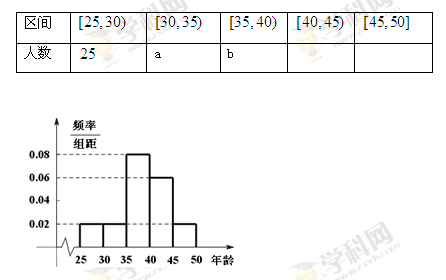
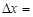 本月价格指数
本月价格指数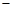 上月价格指数.规定:当
上月价格指数.规定:当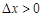 时,称本月价格指数环比增长;
时,称本月价格指数环比增长;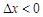 时,称本月价格指数环比下降;当
时,称本月价格指数环比下降;当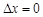 时,称本月价格指数环比持平.
时,称本月价格指数环比持平.