题目内容
在等差数列40,37,34,…中第一个负数项记为ak,则k=
- A.14
- B.13
- C.15
- D.12
C
分析:在等差数列40,37,34,…中,由a1=40,d=-3,得an=40+(n-1)×(-3)=43-3n,由an=43-3n≤0,得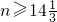 ,由此能求出k的值.
,由此能求出k的值.
解答:在等差数列40,37,34,…中,
∵a1=40,
d=37-40=-3,
∴an=40+(n-1)×(-3)=43-3n,
由an=43-3n≤0,
得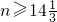 ,
,
∵a14=43-3×14=1,
a15=43-3×15=-2,
∴k=15.
故选C.
点评:本题考查等差数列的通项公式的性质和应用,是基础题.解题时要认真审题,仔细解答.
分析:在等差数列40,37,34,…中,由a1=40,d=-3,得an=40+(n-1)×(-3)=43-3n,由an=43-3n≤0,得
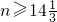 ,由此能求出k的值.
,由此能求出k的值.解答:在等差数列40,37,34,…中,
∵a1=40,
d=37-40=-3,
∴an=40+(n-1)×(-3)=43-3n,
由an=43-3n≤0,
得
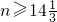 ,
,∵a14=43-3×14=1,
a15=43-3×15=-2,
∴k=15.
故选C.
点评:本题考查等差数列的通项公式的性质和应用,是基础题.解题时要认真审题,仔细解答.

练习册系列答案
相关题目
在等差数列40,37,34,…中第一个负数项是( )
| A、第13项 | B、第14项 | C、第15项 | D、第16项 |