题目内容
求函数y＝
，x∈[－4，2]的单调区间．
答案：
解析：
解析：
|
解：令y＝ 因为函数y＝ 又二次函数u＝－x2－2x＋8在[－4，－1]上单调递增，在(－1，2]上单调递减， 所以，函数y＝ 点评：研究函数的单调性问题必须在其定义域范围内加以考虑．讨论复合函数的单调性也离不开其定义域，单调区间必须是定义域的子区间．复合函数的单调性问题，一般都要转化为基本初等函数的单调性问题来解决，而二次函数是其中重点考查的一类函数． |
，u＝－x2－2x＋8＝－(x＋1)2＋9．
在[0，＋∞)上单调递增，
(x∈[－4，2])的单调递增区间是[－4，－1]，单调递减区间是(－1，2]．
练习册系列答案
相关题目
函数
函数
．
(A＞0，ω＞0，|φ|＜
，x∈R)的图象的一部分如图所示.
]时，求函
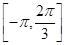上的函数y＝f(x)的图象关于直线x＝－
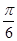对称，当x∈
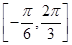时，函数f(x)＝Asin(ωx＋φ) 
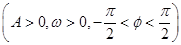的图象如图所示．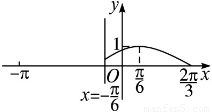
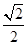的解．
满足：
记y＝f(x)． 
不等式｜a－lnx｜－ln[f '(x)－3x]＞0恒成立，求实数a的取值范围：