题目内容
已知曲线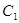 的方程是
的方程是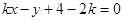
 ,曲线
,曲线 的方程是
的方程是
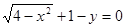 ,给出下列结论:
,给出下列结论:
①曲线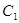 恒过定点
恒过定点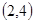 ;
;
 ②曲线
②曲线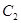 的图形是一个圆;
的图形是一个圆;
③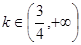 时,
时,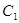 与
与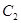 有一个公共点;
④若
有一个公共点;
④若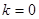 时,则
时,则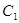 与
与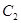 必无公共点。
必无公共点。
其中正确结论的序号是_____________。
【答案】
①③④
【解析】
试题分析:曲线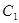 的方程
的方程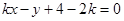 可化为
可化为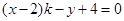 ,所以恒过定点
,所以恒过定点
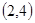 ,所以①正确;曲线
,所以①正确;曲线 的方程
的方程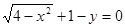 通过移项、平方可以化成
通过移项、平方可以化成
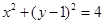 ,但此时
,但此时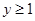 ,所以表示的不是一个完整的圆,二是一个半圆,所以②
,所以表示的不是一个完整的圆,二是一个半圆,所以②
错误;半圆圆心到直线的距离等于半径时,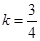 ,结合图象可知,当
,结合图象可知,当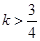 时,直线与
时,直线与
半圆相交或相切,所以有一个公共点,所以③正确;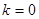 时,直线与半圆相离,所以
时,直线与半圆相离,所以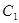
与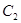 必无公共点,所以④正确.
必无公共点,所以④正确.
考点:本小题主要考查含参数的直线过定点与直线和圆(半圆)的位置关系问题,考查了学生数形结合解决问题的能力和思维的严密性.
点评:含参数的直线方程过定点要灵活应用,化简方程时,要注意化简的等价性,比如本题中的曲线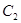 表示的是一个半圆而不是一个完整的圆.
表示的是一个半圆而不是一个完整的圆.

练习册系列答案
相关题目
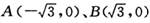 ,P为动点, 且
,P为动点, 且 .记动点P的轨迹为曲E
.记动点P的轨迹为曲E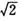 ,l与曲线E相交于不同的两点G、H, 问
,l与曲线E相交于不同的两点G、H, 问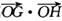 的值是否为定值?若为定值,求出此定值;
若不是, 请说明理由.
的值是否为定值?若为定值,求出此定值;
若不是, 请说明理由. 的参数方程为
的参数方程为 (t为参数),曲线C的极坐标方程是
(t为参数),曲线C的极坐标方程是 以极点为原点,极轴为x轴正方向建立直角坐标系,点
以极点为原点,极轴为x轴正方向建立直角坐标系,点 ,直线
,直线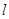 的参数方程为
的参数方程为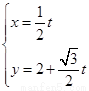 (t为参数),曲线C的极坐标方程是
(t为参数),曲线C的极坐标方程是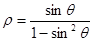 以极点为原点,极轴为x轴正方向建立直角坐标系,点
以极点为原点,极轴为x轴正方向建立直角坐标系,点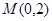 ,直线
,直线 的参数方程为
的参数方程为 (t为参数),曲线C的极坐标方程是
(t为参数),曲线C的极坐标方程是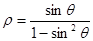 以极点为原点,极轴为x轴正方向建立直角坐标系,点
以极点为原点,极轴为x轴正方向建立直角坐标系,点 ,直线
,直线 的参数方程为
的参数方程为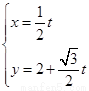 (t为参数),曲线C的极坐标方程是
(t为参数),曲线C的极坐标方程是 以极点为原点,极轴为x轴正方向建立直角坐标系,点
以极点为原点,极轴为x轴正方向建立直角坐标系,点 ,直线
,直线