题目内容
已知函f(x)数满足f(x+1)=-f(x),当x∈(0,1)时,f(x)=2x,则x∈(-3,-2)时,f(x)=
-2x+3
-2x+3
.分析:由f(x+1)=-f(x)得函数的周期性,求x∈(-3,-2)的解析式转化成(0,1)范围内,代入已知解析式即得.
解答:解:∵f(x+1)=-f(x)
∴f(x+2)=f(x)即f(x)是周期为2的函数
设x∈(-3,-2)则x+3∈(0,1)
∴f(x+3)=f(x+1)=-f(x)=2x+3,
即f(x)=-2x+3
故答案为-2x+3
∴f(x+2)=f(x)即f(x)是周期为2的函数
设x∈(-3,-2)则x+3∈(0,1)
∴f(x+3)=f(x+1)=-f(x)=2x+3,
即f(x)=-2x+3
故答案为-2x+3
点评:本题主要考查了利用周期性求解函数解析式,通过未知转化到已知进行求解,属于基础题.

练习册系列答案
相关题目
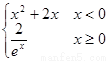 ,则f(x)的“姊妹点对”有 个。
,则f(x)的“姊妹点对”有 个。


 ,函数
,函数
 ,
, ),n=(
),n=( ,
, 的值;
的值;