题目内容
有一块边长为6m的正方形钢板,将其四个角各截去一个边长为x的小正方形,然后焊接成一个无盖的蓄水池.(Ⅰ)写出以x为自变量的容积V的函数解析式V(x),并求函数V(x)的定义域;
(Ⅱ)指出函数V(x)的单调区间;
(Ⅲ)蓄水池的底边为多少时,蓄水池的容积最大?最大容积是多少?
【答案】分析:(Ⅰ)设蓄水池的底面边长为a,则a=6-2x,则蓄水池的容积为:V(x)=x(6-2x)2.由此能写出以x为自变量的容积V的函数解析式V(x),并求出函数V(x)的定义域;
(Ⅱ)由V(x)=x(6-2x)2=4x3-24x2+36x得V'(x)=12x2-48x+36.由此能求出函数V(x)的单调区间;
(Ⅲ)令V'(x)=12x2-48x+36=0,得x=1或x=3(舍).并求得V(1)=16.由V(x)的单调性知,16为V(x)的最大值.由此能求出蓄水池的底边为多少时,蓄水池的容积最大和最大容积是多少.
解答:解:(Ⅰ)设蓄水池的底面边长为a,
则a=6-2x,
则蓄水池的容积为:V(x)=x(6-2x)2.
由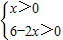 ,
,
得函数V(x)的定义域为x∈(0,3).(4分)
(Ⅱ)由V(x)=x(6-2x)2=4x3-24x2+36x,
得V'(x)=12x2-48x+36.
令V'(x)=12x2-48x+36>0,
解得x<1或x>3;
令V'(x)=12x2-48x+36<0,解得1<x<3.
∵函数V(x)的定义域为x∈(0,3),
∴函数V(x)的单调增区间是:(0,1);函数V(x)的单调减区间是:(1,3).
(Ⅲ)令V'(x)=12x2-48x+36=0,
得x=1或x=3(舍).
并求得V(1)=16.
由V(x)的单调性知,16为V(x)的最大值.
故蓄水池的底边为4m时,蓄水池的容积最大,其最大容积是16m3.(12分)
点评:本题考查函数模型的选择与应用,解题时要认真审题,注意挖掘题设中的隐含条件,合理地运用导数解题.易错点是理不清数量间的相互关系,不能正确地建立方程.再求单调区间时要注意函数的定义域.
(Ⅱ)由V(x)=x(6-2x)2=4x3-24x2+36x得V'(x)=12x2-48x+36.由此能求出函数V(x)的单调区间;
(Ⅲ)令V'(x)=12x2-48x+36=0,得x=1或x=3(舍).并求得V(1)=16.由V(x)的单调性知,16为V(x)的最大值.由此能求出蓄水池的底边为多少时,蓄水池的容积最大和最大容积是多少.
解答:解:(Ⅰ)设蓄水池的底面边长为a,
则a=6-2x,
则蓄水池的容积为:V(x)=x(6-2x)2.
由
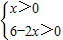 ,
,得函数V(x)的定义域为x∈(0,3).(4分)
(Ⅱ)由V(x)=x(6-2x)2=4x3-24x2+36x,
得V'(x)=12x2-48x+36.
令V'(x)=12x2-48x+36>0,
解得x<1或x>3;
令V'(x)=12x2-48x+36<0,解得1<x<3.
∵函数V(x)的定义域为x∈(0,3),
∴函数V(x)的单调增区间是:(0,1);函数V(x)的单调减区间是:(1,3).
(Ⅲ)令V'(x)=12x2-48x+36=0,
得x=1或x=3(舍).
并求得V(1)=16.
由V(x)的单调性知,16为V(x)的最大值.
故蓄水池的底边为4m时,蓄水池的容积最大,其最大容积是16m3.(12分)
点评:本题考查函数模型的选择与应用,解题时要认真审题,注意挖掘题设中的隐含条件,合理地运用导数解题.易错点是理不清数量间的相互关系,不能正确地建立方程.再求单调区间时要注意函数的定义域.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目