题目内容
如下图,等边△ABC的边长为4,D为BC中点,沿AD把△ADC折叠到△ADC′处,使二面角BADC′?为60°,则折叠后点A到直线BC′的距离为_________;二面角ABC′D的正切值为__________.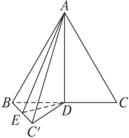
答案:![]() 2
2

解析:(1)取BC′中点E,连结AE、DE,则AE即为A到BC′的距离.
∵△ABC为等边三角形,边长为4,
故AD=![]() .
.
∵BD⊥AD,DC′⊥AD,则∠BDC′即为二面角BADC′的平面角.
∴∠BDC′=60°,BD=DC′=2,则DE=![]() .
.
又∵AD⊥面BDE,则AD⊥DE,
∴![]() .
.
(2)DE⊥BC′,AE⊥BC′,则∠AED即为二面角ABC′D的平面角.
∴tan∠AED=![]() =2,即二面角ABC′D的正切值为2.
=2,即二面角ABC′D的正切值为2.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目