题目内容
设 均为正实数,且
均为正实数,且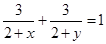 ,则
,则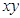 的最小值为 .
的最小值为 .
【答案】
16
【解析】
试题分析:首先,由于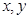 均为正实数,则
均为正实数,则 ,因此
,因此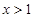 ,同理
,同理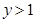 .求
.求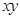 的最小值,这里有两个参数,如能减少一个参数,就可把式子化为一个参数的式子,便于找到解题思路.由已知解出
的最小值,这里有两个参数,如能减少一个参数,就可把式子化为一个参数的式子,便于找到解题思路.由已知解出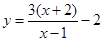 ,那么
,那么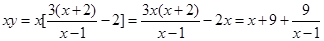 ,
,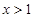 时,
时,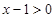 ,
,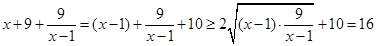 ,当且仅当
,当且仅当 ,即
,即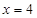 时等号成立,故所求最小值为16.
时等号成立,故所求最小值为16.
考点:基本不等式的应用.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案
相关题目
 均为正实数,且
均为正实数,且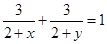 ,则
,则 的最小值为 .
的最小值为 . 均为正实数,且
均为正实数,且 ,则
,则 的最小值为 .
的最小值为 .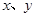 均为正实数,且
均为正实数,且 ,则
,则 的最小值为 .
的最小值为 . 均为正实数,且
均为正实数,且 ,则
,则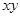 的最小值为____________.
的最小值为____________.