题目内容
(08年金华一中理) 15分) 已知函数![]() ,满足:
,满足:
①对任意![]() 都有
都有![]() ;②对任意
;②对任意![]() 都有
都有![]() .
.
(1)试证明:![]() 为
为![]() 上的单调增函数;
上的单调增函数;
(2)求![]() ;
;
(3)令![]() ,试证明:
,试证明:![]()
解析: 解:(1)由①知,对任意![]() ,都有
,都有![]() ,
,
由于![]() ,从而
,从而![]() ,所以函数
,所以函数![]() 为
为![]() 上的单调增函数. 3分
上的单调增函数. 3分
(2)令![]() ,则
,则![]() ,显然
,显然![]() ,否则
,否则![]() ,与
,与![]() 矛盾.从而
矛盾.从而![]() ,而由
,而由![]() ,即得
,即得![]() .
.
又由(I)知![]() ,即
,即![]() .
.
于是得![]() ,又
,又![]() ,从而
,从而![]() ,即
,即![]() . 5分
. 5分
进而由![]() 知,
知,![]() .
.
于是![]() , 7分
, 7分
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
由于![]() ,
,
而且由(I)知,函数![]() 为单调增函数,因此
为单调增函数,因此![]() .
.
从而![]() . 9分
. 9分
(3)![]() ,
,
![]() ,
,![]() .
.
即数列![]() 是以6为首项, 以3为公比的等比数列 .
是以6为首项, 以3为公比的等比数列 .
∴ ![]() . 11分
. 11分
于是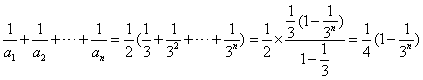 ,
,
显然![]() , 12分
, 12分
另一方面![]() ,
,
从而![]() .
.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目