题目内容
14.一个圆经过圆C1:x2+y2-8x-9=0和圆C2:x2+y2-8y+15=0的两个交点,且圆心在直线2x-y-1=0上,求该圆的方程.分析 利用“圆系”方程的概念求圆的方程,于是可设所求圆的方程为x2+y2-8x-9+λ(x2+y2-8y+15)=0(λ≠-1),得到其圆心坐标,再代入2x-y-1=0可得出λ的值,反代入圆系方程化简得出圆的方程来.
解答 解:设所求圆的方程为x2+y2-8x-9+λ(x2+y2-8y+15)=0(λ≠-1).
可知圆心坐标为($\frac{4}{1+λ}$,$\frac{4λ}{1+λ}$).
因圆心在直线2x-y-1=0上,所以2×$\frac{4}{1+λ}$-$\frac{4λ}{1+λ}$-1=0,解得λ=$\frac{7}{5}$.
将λ=$\frac{7}{5}$代入所设方程并化简,求圆的方程x2+y2-$\frac{10}{3}$x-$\frac{14}{3}$y+5=0.
点评 本题考查直线和圆的方程,直线与圆的位置关系,考查了圆的几何性质,圆的方程的求法--待定系数法求方程的思想方法,圆系方程的概念.

练习册系列答案
相关题目
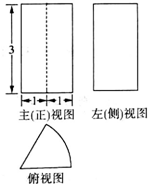 某圆柱切割获得的几何体的三视图如图所示,其中俯视图是中心角为$\frac{π}{3}$的扇形,则该几何体的体积为2π.
某圆柱切割获得的几何体的三视图如图所示,其中俯视图是中心角为$\frac{π}{3}$的扇形,则该几何体的体积为2π.