题目内容
已知椭圆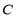 的两个焦点分别为
的两个焦点分别为 ,
, ,短轴的两个端点分别为
,短轴的两个端点分别为 ,
, .
.
(1)若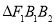 为等边三角形,求椭圆
为等边三角形,求椭圆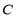 的方程;
的方程;
(2)若椭圆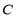 的短轴长为2,过点
的短轴长为2,过点 的直线
的直线 与椭圆
与椭圆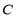 相交于
相交于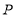 、
、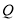 两点,且
两点,且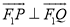 ,求直线
,求直线 的方程.
的方程.
练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
题目内容
已知椭圆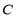 的两个焦点分别为
的两个焦点分别为 ,
, ,短轴的两个端点分别为
,短轴的两个端点分别为 ,
, .
.
(1)若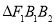 为等边三角形,求椭圆
为等边三角形,求椭圆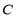 的方程;
的方程;
(2)若椭圆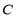 的短轴长为2,过点
的短轴长为2,过点 的直线
的直线 与椭圆
与椭圆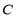 相交于
相交于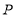 、
、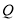 两点,且
两点,且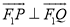 ,求直线
,求直线 的方程.
的方程.
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案