Question

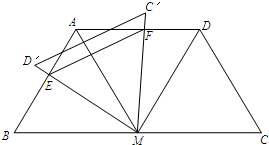（2012•大丰市一模）已知：如图，M是线段BC的中点，BC=4，分别以MB、MC为边在线段BC的同侧作等边△BAM、等边△MCD，连接AD．
（1）求证：四边形ABCD是等腰梯形；
（2）将△MDC绕点M逆时针方向旋转α（60°＜α＜120°），得到△MD′C′，MD′交AB于点E，MC′交AD于点F，连接EF．
①求证：EF∥D′C′；
②△AEF的周长是否存在最小值？如果不存在，请说明理由；如果存在，请计算出△AEF周长的最小值．

Answer 1

分析：（1）可求出∠AMD=60°，MA=MD，继而得出△AMD是等边三角形，根据∠ADM=∠DMC=60°，可判断AD∥BC，从而可得出结论；
（2）先证△MDF全等于△MAE，可得△MEF为等边三角形，即得EF∥D?C?；
（3）由①可得AE+AF=AB，为定值，只需满足EF最小即可，由①可得△MEF为等边三角形，EF=ME，故只需ME最小即可，显然当ME⊥AB的时候ME最小．

解答：证明：（1）∵M是线段BC的中点，
∴BM=MC，
又∵△BAM、△MCD是等边三角形，
∴∠AMB=∠DMC=60°，MA=MD，
∴△MAD为等边三角形，
∴∠ADM=∠DMC=60°，
∴AD∥BC，
又∵AB=BM=MC=DC，
∴四边形ABCD为等腰梯形． 
（2）①∵∠DMF+∠AMF=60°，∠AME+∠AMF=60°，
∴∠AME=∠DMF，
∵在△MAE和△MDF中，

∠AME=∠DMF ∠EAM=∠FDM MA=MD

，
∴△MAE≌△MDF（AAS），
∴ME=MF，
∴∠EMF=∠AMF+∠AME=∠AMF+∠DMF=∠AMD=60°，
∴△MEF为等边三角形，
∴∠FEM=∠C'D'M=60°，
∴EF∥D′C′．
解：②存在最小值．
由①得，AE+AF=AB，为定值，只需满足EF最小即可，
由①得，△MEF是等边三角形，EF=ME，只需满足ME最小即可，
显然当ME⊥AB时取得最小，
由等边三角形的性质可得：此时ME=2

3

，
故△AEF的周长最小值等于2+

3

点评：本题考查了四边形综合题，涉及了全等三角形的判定与性质、旋转的性质及等腰梯形的判定，解答本题要求我们熟练掌握各个知识点，并能将所学知识融会贯通．