题目内容
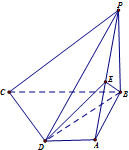
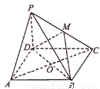
如图,四棱锥P--ABCD中,PB⊥底面ABCD.底面ABCD为直角梯形,AD∥BC,AB=AD=PB=3,BC=6.点E在棱PA上,且PE=2EA.
(1)求异面直线PA与CD所成的角;
(2)求证:PC∥平面EBD;
(3)求二面角A-BE--D的余弦值.
分析:(1)以点B为坐标原点,以BA为x轴,以BC为y轴,以BP为z轴,建立空间直角坐标至B-xyz,利用两个向量的所成角即为异面直线CD与PA所成的角,可得结论;
(2)欲证PC∥平面EBD,根据直线与平面平行的判定定理可知只需证PC与平面EBD内一直线平行连接AC交BD于G,连接EG,根据比例关系可知PC∥EG,而EG?平面EBD,PC?平面EBD,满足定理所需条件;
(3)先求平面EBD的法向量与平面ABE的法向量,然后利用向量的夹角公式求出此角的余弦值即二面角A-BE-D的大小的余弦值.
解答:(1)解:如图,以点B为坐标原点,以BA为x轴,以BC为y轴,以BP为z轴,建立空间直角坐标系B-xyz.
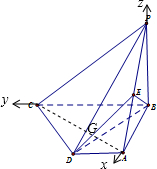
设BC=a,则A(3,0,0),P(0,0,3),D(3,3,0),C(0,6,0)
∴
=(3,-3,0),
=(3,0,-3)
∴cos<
,>=
=
=
,
因此异面直线CD与PA所成的角为60°;
(2)证明:连接AC交BD于G,连接EG.
∵
==,
=,∴
=∴PC∥EG
又∵EG?平面EBD,PC?平面EBD
∴PC∥平面EBD;
(3)解:设平面EBD的法向量为
=(x,y,1),
设E(a,0,c),则∵PE=2EA,∴(a,0,c-3)=2(3-a,0,-c)
∴a=2,c=1,∴E(2,0,1)
∴
=(2,0,1),
∵
=(3,3,0)
∴由
,可得x=-
,y=
∴
=(-
,
,1)
又∵平面ABE的法向量为
=(0,1,0),
∴cos(
,)=
=
.
即二面角A-BE-D的大小的余弦值为
.
点评:本题主要考查直线与平面的位置关系、两异面直线所成角、二面角及其平面角等有关知识,考查空间想象能力和思维能力,应用向量知识解决立体几何问题的能力.
练习册系列答案
相关题目
 如图,四棱锥P--ABCD中,PB⊥底面ABCD.底面ABCD为直角梯形,AD∥BC,AB=AD=PB=3,BC=6.点E在棱PA上,且PE=2EA.
如图,四棱锥P--ABCD中,PB⊥底面ABCD.底面ABCD为直角梯形,AD∥BC,AB=AD=PB=3,BC=6.点E在棱PA上,且PE=2EA.


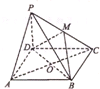 如图,四棱锥P-A BCD中,底面ABCD为菱形,BD⊥面PAC,A C=10,PA=6,cos∠PCA=
如图,四棱锥P-A BCD中,底面ABCD为菱形,BD⊥面PAC,A C=10,PA=6,cos∠PCA=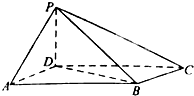 如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD,PD⊥底面ABCD.
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD,PD⊥底面ABCD. 如图,四棱锥P-ABCD中,PA⊥底面ABCD,PC⊥AD.底面ABCD为梯形,AB∥DC,AB⊥BC.PA=AB=BC,点E在棱PB上,且PE=2EB.
如图,四棱锥P-ABCD中,PA⊥底面ABCD,PC⊥AD.底面ABCD为梯形,AB∥DC,AB⊥BC.PA=AB=BC,点E在棱PB上,且PE=2EB.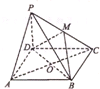 如图,四棱锥P-A BCD中,底面ABCD为菱形,BD⊥面PAC,A C=10,PA=6,cos∠PCA=
如图,四棱锥P-A BCD中,底面ABCD为菱形,BD⊥面PAC,A C=10,PA=6,cos∠PCA= ,M是PC的中点.
,M是PC的中点. ,M是PC的中点.
,M是PC的中点.