题目内容
与数列交汇.例3:已知m,n,m+n成等差数列,m,n,mn成等比数列,则椭圆| x2 |
| m |
| y 2 |
| n |
分析:由等差中项与等比中项,列方程组可解得m,n的值,再求椭圆的离心率即可.
解答:解:
?
(n≠0),
∴m2=2m,又m≠0,得m=2,n=4
∴椭圆为
+
=1,
c2=4-2=2,得c=
,又a=2,
∴e=
=
.
故答案为:
.
|
|
∴m2=2m,又m≠0,得m=2,n=4
∴椭圆为
| x2 |
| 2 |
| y 2 |
| 4 |
c2=4-2=2,得c=
| 2 |
∴e=
| c |
| a |
| ||
| 2 |
故答案为:
| ||
| 2 |
点评:表面看题意涉及的知识点较多,但经分析后,运用一些基本的概念与知识即可解答.

练习册系列答案
相关题目
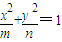 的离心率是 .
的离心率是 .