��Ŀ����
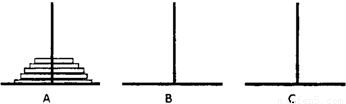
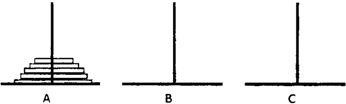 ��ŵ�������Ǹ���һ����˵�γɵ�һ�����⣺���������Ӻ�����һ�������ϵ����ɴ�С���ȵĴ���Բ�̣������й���Բ�̴�һ��������ȫ���Ƶ���һ�������ϣ�
��ŵ�������Ǹ���һ����˵�γɵ�һ�����⣺���������Ӻ�����һ�������ϵ����ɴ�С���ȵĴ���Բ�̣������й���Բ�̴�һ��������ȫ���Ƶ���һ�������ϣ���ÿ��ֻ���ƶ�1����Ƭ���ڴ��̲��ܵ���С�����森
��ͼ��ʾ����A�������е�Ƭ�Ƶ�C���ϣ�B�˿�����Ϊ���ɸ�ʹ�ã��ƽ���Ƭ��һ�������ƶ�����һ������Ϊ�ƶ�һ�Σ��ǽ�A�����ϵ�n����Ƭ�ƶ���C����������Ҫ�ƶ�an�Σ�
����д��a1��a2��a3��a4��ֵ��
����������{an}��ͨ�ʽ��
������bn=
| n | an+1 |
����������n=1ʱ����A���Ƶ�C������һ�ַ���A��C����a1=1����n=2ʱ����A���Ƶ�C���Ϸ�3������A��B��A��C��B��C�������ַ�������a2=3����n=3ʱ����A���Ƶ�C���Ϸ��߲�����A��C��A��B��C��B��A��C��B��A��B��C��A��C�������ַ�������a3=7��ͬ������a4=15��
�����ɣ���������{an}��ͨ�ʽΪan=2n-1��������ѧ���ɷ�֤��������֤n=1ʱ��an�������ڼ��赱n=k��k��1��ʱ��ak=2k-1������֤����n=k+1ʱ��ak+1=2k+1-1Ҳ��������֤������{an}��ͨ�ʽ��an=2n-1��
�����ɣ���֪��an=2n-1��bn=
=
=n•(
)n������sn=1•
+2•(
)2+3•(
)3+��+n•(
)n����
sn=1•(
)2+2•(
)3+3•(
)4+��+n•(
)n+1����ʽ�������
sn���Ӷ���sn��
�����ɣ���������{an}��ͨ�ʽΪan=2n-1��������ѧ���ɷ�֤��������֤n=1ʱ��an�������ڼ��赱n=k��k��1��ʱ��ak=2k-1������֤����n=k+1ʱ��ak+1=2k+1-1Ҳ��������֤������{an}��ͨ�ʽ��an=2n-1��
�����ɣ���֪��an=2n-1��bn=
| n |
| an+1 |
| n |
| 2n |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
����⣺���������⣬֪a1=1��a2=3��a3=7��a4=15��
�����ɣ����Ʋ⣬����{an}��ͨ�ʽΪan=2n-1��
��������ѧ���ɷ�֤�����£�
�ٵ�n=1ʱ����A���Ƶ�C����ֻ��һ�ַ�������a1=1����ʱan=1=21-1������
�ڼ��赱n=k��k��1��ʱ��ak=2k-1������
��n=k+1ʱ����A���ϵ�k+1����Ƭ������k����Ƭ����ײ�1�ŵ�Ƭ��ɵģ��ɼ����֪����A���ϵ�k����Ƭ�Ƶ�B������ak=2k-1�ַ������ٽ���ײ�1�ŵ�Ƭ�Ƶ�C������1���Ʒ������B���ϵ�k����Ƭ�Ƶ�C���ϣ���ʱ�ײ���һ�����ĵ�Ƭ������ak=2k-1���ƶ��������ʴ�A���ϵ�k+1����Ƭ�Ƶ�C���Ϲ���ak+1=ak+1+ak=2ak+1=2��2k-1��+1=2k+1-1���ƶ�������
���Ե�n=k+1ʱ��an=2n-1������
�ɢ٢ڿ�֪����{an}��ͨ�ʽ��an=2n-1��
�����ɣ���֪��an=2n-1�����ԣ�bn=
=
=n•(
)n��
��sn=1•
+2•(
)2+3•(
)3+��+n•(
)n�٣�
sn=1•(
)2+2•(
)3+3•(
)4+��+n•(
)n+1�ڣ�
��-�ڣ���(1-
)sn=
+(
)2+(
)3+��+(
)n-n•(
)n+1��
��
Sn=
-n•(
)n+1��
��Sn=2-(n+2)•(
)n��
�����ɣ����Ʋ⣬����{an}��ͨ�ʽΪan=2n-1��
��������ѧ���ɷ�֤�����£�
�ٵ�n=1ʱ����A���Ƶ�C����ֻ��һ�ַ�������a1=1����ʱan=1=21-1������
�ڼ��赱n=k��k��1��ʱ��ak=2k-1������
��n=k+1ʱ����A���ϵ�k+1����Ƭ������k����Ƭ����ײ�1�ŵ�Ƭ��ɵģ��ɼ����֪����A���ϵ�k����Ƭ�Ƶ�B������ak=2k-1�ַ������ٽ���ײ�1�ŵ�Ƭ�Ƶ�C������1���Ʒ������B���ϵ�k����Ƭ�Ƶ�C���ϣ���ʱ�ײ���һ�����ĵ�Ƭ������ak=2k-1���ƶ��������ʴ�A���ϵ�k+1����Ƭ�Ƶ�C���Ϲ���ak+1=ak+1+ak=2ak+1=2��2k-1��+1=2k+1-1���ƶ�������
���Ե�n=k+1ʱ��an=2n-1������
�ɢ٢ڿ�֪����{an}��ͨ�ʽ��an=2n-1��
�����ɣ���֪��an=2n-1�����ԣ�bn=
| n |
| 2n-1+1 |
| n |
| 2n |
| 1 |
| 2 |
��sn=1•
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
��-�ڣ���(1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
��
| 1 |
| 2 |
| ||||
1-
|
| 1 |
| 2 |
��Sn=2-(n+2)•(
| 1 |
| 2 |
���������⿼��������֪ʶ����ѧ���ɷ����ۺ�Ӧ�ã�����ѧ���ɷ�֤��ʱ��Ҫ���գ�1����֤����2�����裬��3��֤���IJ����𣬱��⣨����������ͷ�������̲����Ƶ��ȱ�����ǰn���ʽһ�����Ǵ�λ�������

��ϰ��ϵ�д�
�����Ŀ
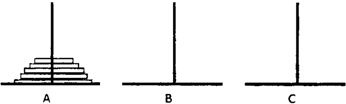 ��ŵ�������Ǹ���һ����˵�γɵ�һ�����⣺���������Ӻ�����һ�������ϵ����ɴ�С���ȵĴ���Բ�̣������й���Բ�̴�һ��������ȫ���Ƶ���һ�������ϣ�
��ŵ�������Ǹ���һ����˵�γɵ�һ�����⣺���������Ӻ�����һ�������ϵ����ɴ�С���ȵĴ���Բ�̣������й���Բ�̴�һ��������ȫ���Ƶ���һ�������ϣ�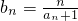 ��������{bn}��ǰn���Sn��
��������{bn}��ǰn���Sn��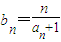 ��������{bn}��ǰn���Sn��
��������{bn}��ǰn���Sn��