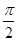题目内容
已知向量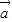 ,
,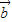 满足
满足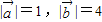 ,且
,且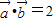 ,则
,则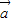 与
与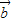 的夹角为 .
的夹角为 .
【答案】分析:根据向量数量积的定义,结合题中数据直接利用向量的夹角公式,算出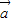 与
与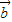 的夹角余弦值为
的夹角余弦值为 ,结合两个向量夹角的取值范围,即可得到
,结合两个向量夹角的取值范围,即可得到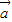 与
与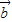 的夹角的大小.
的夹角的大小.
解答:解:∵向量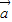 ,
,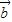 满足
满足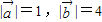 ,且
,且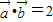 ,
,
∴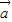 与
与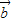 的夹角θ满足:cosθ=
的夹角θ满足:cosθ=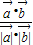 =
=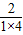 =
=
∵θ∈[0,π],∴θ=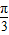
故答案为: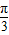
点评:本题给出两个向量的模与数量积,求它们夹角大小.着重考查了平面向量数量积的定义与向量夹角公式等知识,属于基础题.
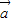 与
与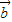 的夹角余弦值为
的夹角余弦值为 ,结合两个向量夹角的取值范围,即可得到
,结合两个向量夹角的取值范围,即可得到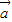 与
与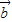 的夹角的大小.
的夹角的大小.解答:解:∵向量
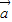 ,
,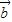 满足
满足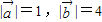 ,且
,且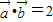 ,
,∴
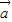 与
与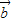 的夹角θ满足:cosθ=
的夹角θ满足:cosθ=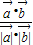 =
=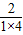 =
=
∵θ∈[0,π],∴θ=
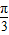
故答案为:
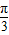
点评:本题给出两个向量的模与数量积,求它们夹角大小.着重考查了平面向量数量积的定义与向量夹角公式等知识,属于基础题.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
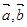 ,满足
,满足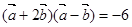 ,且
,且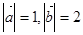 ,则
,则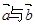 的夹角为( )
的夹角为( )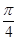 B.
B.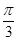 C.
C.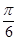 D.
D.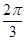
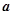 ,
,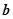 满足
满足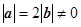 ,且关于
,且关于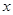 的函数
的函数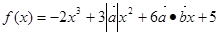 在实数集R上是单调递减函数,则向量
在实数集R上是单调递减函数,则向量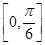 B
B 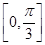 C
C
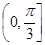 D
D
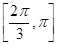
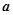 ,
,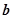 满足
满足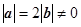 ,且关于
,且关于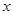 的函数
的函数 在实数集
在实数集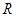 上单调递增,则向量
上单调递增,则向量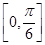 B.
B.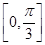 C.
C.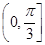 D.
D.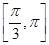
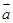 、
、 满足
满足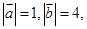 ,且
,且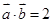 ,则
,则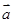 与
与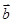 的夹角为( )
的夹角为( )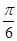 B.
B. C.
C.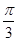 D.
D.