题目内容
已知椭圆W的中心在原点,焦点在X轴上,离心率为
,椭圆短轴的一个端点与两焦点构成的三角形的面积为2
,椭圆W的左焦点为F,过x轴的一点M(-3,0)任作一条斜率不为零的直线L与椭圆W交于不同的两点A、B,点A关于X轴的对称点为C.
(1)求椭圆W的方程;
(2)求证:
=λ
(λ∈R);
(3)求△MBC面积S的最大值.
分析:(Ⅰ)根据离心率,准线和a,b和c的关系,联立方程求得a,b和c.椭圆的方程可得.
(Ⅱ)可设直线l的方程为y=k(x+3),点A,B的坐标分别为(x1,y1),(x2,y2),则点C的坐标为(x1,-y1),y1=k(x1+3),y2=k(x2+3).进而根据椭圆的第二定义得,判断出B,F,C三点共线,
(Ⅲ)根据三角形面积公式求得S的表达式,根据k的范围确定S的范围.
解答: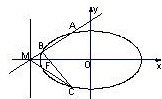
解:(Ⅰ)设椭圆W的方程为
+=1(a>b>0),由题意可知
,解得
a=,b=,c=2.
所以椭圆W的方程为
+=1.
(Ⅱ)点M坐标为(-3,0),于是可设直线l的方程为y=k(x+3),点A,B的坐标分别为(x
1,y
1),(x
2,y
2),
则点C的坐标为(x
1,-y
1),y
1=k(x
1+3),y
2=k(x
2+3),由椭圆的第二定义可得
==,
所以B,F,C三点共线,即
=λ
(λ∈R).
(Ⅲ)由题意知
S=|MF||y1|+|MF||y2|=|MF||y1+y2|=
|MF||k(x1+x2)+6k|.
又由M(-3,0),F(-2,0),则|MF|=1,
S==≤=,
当且仅当
k2=时,“=”成立,
所以△MBC面积S的最大值为
.
点评:本题主要考查了椭圆的方程和性质,以及直线与椭圆的位置关系,知识点多,复杂难懂,应熟练掌握椭圆的一些基本性质.
练习册系列答案
相关题目
 解:(Ⅰ)设椭圆W的方程为
解:(Ⅰ)设椭圆W的方程为 解:(Ⅰ)设椭圆W的方程为
解:(Ⅰ)设椭圆W的方程为
 已知椭圆W的中心在原点,焦点在x轴上,离心率为
已知椭圆W的中心在原点,焦点在x轴上,离心率为 (2012•南宁模拟)已知椭圆W的中心在原点,焦点在x轴上,离心率为
(2012•南宁模拟)已知椭圆W的中心在原点,焦点在x轴上,离心率为