题目内容
数轴上有一列点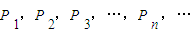 ,已知当n≥2时,点
,已知当n≥2时,点 是把线段
是把线段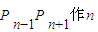 等分的分点中最靠近
等分的分点中最靠近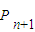 的点,设线段
的点,设线段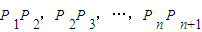 的长度分别为
的长度分别为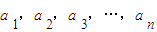 ,其中
,其中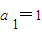 .
.(Ⅰ)写出
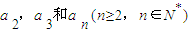 的表达式;
的表达式;(Ⅱ)证明
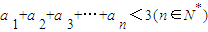 ;
;(Ⅲ)设点
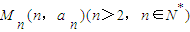 ,在这些点中是否存在两个点同时在函数
,在这些点中是否存在两个点同时在函数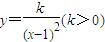 的图象上,如果存在,请求出点的坐标;如果不存在,请说明理由.
的图象上,如果存在,请求出点的坐标;如果不存在,请说明理由.
【答案】分析:(Ⅰ)依题意当n≥2时,Pn-1Pn=(n-1)PnPn+1,结合已知可得an与an-1的递推公式,结合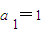 ,代入即可求解
,代入即可求解
(Ⅱ)由(I)可知,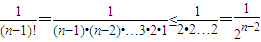 ,利用放缩法,结合等比数列的求和公式可证
,利用放缩法,结合等比数列的求和公式可证
(Ⅲ)先假设存在两个点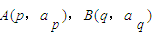 都在函数
都在函数 的图象上,把点的 坐标代入可得
的图象上,把点的 坐标代入可得 ,然后进行推理,即可判断
,然后进行推理,即可判断
解答:解:(Ⅰ)依题意当n≥2时,有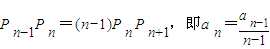 ,
,
∵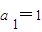 ,
,
∴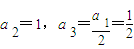 ,
, ,
,
故 .
.
(Ⅱ)证明:因为当n≥2时, ,
,
∴
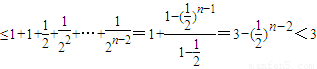
故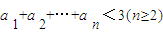 ,
,
而 显然成立,
显然成立,
故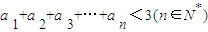 ;
;
(Ⅲ)证明:假设存在两个点 (其中p≠q,p,q∈N*,p>2,q>2)都在函数
(其中p≠q,p,q∈N*,p>2,q>2)都在函数 的图象上,
的图象上,
∴ ,
,
即 ,
,
 ,
,
∴ ,
,
∴ 不成立,故不存在满足题设条件的两个点.
不成立,故不存在满足题设条件的两个点.
点评:本题综合考查了数列的递推公式的应用,不等式的放缩法在证明不等式中的应用,等比数列 的求和公式的应用及存在性问题的求解
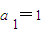 ,代入即可求解
,代入即可求解(Ⅱ)由(I)可知,
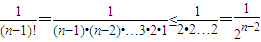 ,利用放缩法,结合等比数列的求和公式可证
,利用放缩法,结合等比数列的求和公式可证(Ⅲ)先假设存在两个点
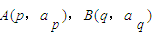 都在函数
都在函数 的图象上,把点的 坐标代入可得
的图象上,把点的 坐标代入可得 ,然后进行推理,即可判断
,然后进行推理,即可判断解答:解:(Ⅰ)依题意当n≥2时,有
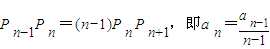 ,
,∵
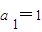 ,
,∴
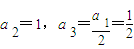 ,
, ,
,故
 .
.(Ⅱ)证明:因为当n≥2时,
 ,
,∴

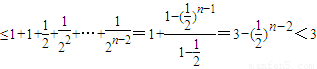
故
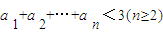 ,
,而
 显然成立,
显然成立,故
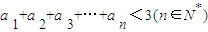 ;
;(Ⅲ)证明:假设存在两个点
 (其中p≠q,p,q∈N*,p>2,q>2)都在函数
(其中p≠q,p,q∈N*,p>2,q>2)都在函数 的图象上,
的图象上,∴
 ,
,即
 ,
, ,
,∴
 ,
,∴
 不成立,故不存在满足题设条件的两个点.
不成立,故不存在满足题设条件的两个点.点评:本题综合考查了数列的递推公式的应用,不等式的放缩法在证明不等式中的应用,等比数列 的求和公式的应用及存在性问题的求解

练习册系列答案
相关题目