题目内容
若四面体ABCD的三组对棱分别相等，即AB=CD，AC=BD，AD=BC，则 （写出所有正确结论编号）①四面体ABCD每组对棱相互垂直
②四面体ABCD每个面的面积相等
③从四面体ABCD每个顶点出发的三条棱两两夹角之和大于90°而小于180°
④连接四面体ABCD每组对棱中点的线段互垂直平分
⑤从四面体ABCD每个顶点出发的三条棱的长可作为一个三角形的三边长．
【答案】分析：①将四面体ABCD的三组对棱分别看作平行六面体的对角线，由于三组对棱分别相等，所以平行六面体为长方体．结合长方体的性质判断
②四面体ABCD的每个面是全等的三角形，面积是相等的．
③由②，从四面体ABCD每个顶点出发的三条棱两两夹角能够等量代换为同一个三角形内的三个内角，它们之和为180°．
④连接四面体ABCD每组对棱中点构成菱形，线段互垂直平分
⑤由①，设所在的长方体长宽高分别为a，b，c，则每个顶点出发的三条棱长分别为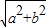
，
，
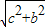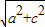易知能构成三角形．
解答：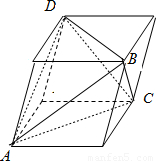
解：①将四面体ABCD的三组对棱分别看作平行六面体的对角线，由于三组对棱分别相等，所以平行六面体为长方体．
由于长方体的各面不一定为正方形，所以同一面上的面对角线不一定垂直，从而每组对棱不一定相互垂直．①错误
②四面体ABCD的每个面是全等的三角形，面积是相等的．②正确
③由②，四面体ABCD的每个面是全等的三角形，从四面体ABCD每个顶点出发的三条棱两两夹角能够等量代换为同一个三角形内的三个内角，它们之和为180°．③错误
④连接四面体ABCD每组对棱中点构成菱形，线段互垂直平分④正确
⑤由①，设所在的长方体长宽高分别为a，b，c，则每个顶点出发的三条棱长分别为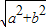
，
，
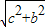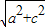，任意两边之和大于第三边，能构成三角形．⑤正确
故答案为：②④⑤
点评：本题考查空间几何体的结构特征，线线位置故选，要具有良好的转化，推理、论证能力．
②四面体ABCD的每个面是全等的三角形，面积是相等的．
③由②，从四面体ABCD每个顶点出发的三条棱两两夹角能够等量代换为同一个三角形内的三个内角，它们之和为180°．
④连接四面体ABCD每组对棱中点构成菱形，线段互垂直平分
⑤由①，设所在的长方体长宽高分别为a，b，c，则每个顶点出发的三条棱长分别为
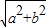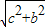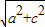，，易知能构成三角形．解答：
解：①将四面体ABCD的三组对棱分别看作平行六面体的对角线，由于三组对棱分别相等，所以平行六面体为长方体．由于长方体的各面不一定为正方形，所以同一面上的面对角线不一定垂直，从而每组对棱不一定相互垂直．①错误
②四面体ABCD的每个面是全等的三角形，面积是相等的．②正确
③由②，四面体ABCD的每个面是全等的三角形，从四面体ABCD每个顶点出发的三条棱两两夹角能够等量代换为同一个三角形内的三个内角，它们之和为180°．③错误
④连接四面体ABCD每组对棱中点构成菱形，线段互垂直平分④正确
⑤由①，设所在的长方体长宽高分别为a，b，c，则每个顶点出发的三条棱长分别为
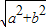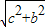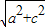，，，任意两边之和大于第三边，能构成三角形．⑤正确故答案为：②④⑤
点评：本题考查空间几何体的结构特征，线线位置故选，要具有良好的转化，推理、论证能力．
练习册系列答案
相关题目