题目内容
若二次函数满足f(x+1)-f(x)=2x且f(0)=1,(1)求f(x)的解析式;
(2)若在R上,不等式f(x)>2x+m恒成立,求实数m的取值范围.
【答案】分析:(1)二次函数满足f(x+1)-f(x)=2x且f(0)=1,设其方程为y=ax2+bx+1,代入f(x+1)-f(x)=2x,整理后利用同一性求出系数,
(2)不等式f(x)>2x+m恒成立,即f(x)-2x-m>0恒成立,由判别式求参数即可
解答:解:(1)由题意,设其方程为y=ax2+bx+1代入f(x+1)-f(x)=2x恒成立,整理得2ax+a+b=2x恒成立,既得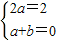 解得
解得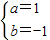
故f(x)=x2-x+1
(2)在R上不等式f(x)>2x+m恒成立,即x2-3x+1-m>0恒成立,故△=9-4(1-m)<0,解得m<-
点评:本题考查函数解析式的求解及常用方法,解题的关键是了解二次函数的解析式的结构利用待定系数法设出解析式,再代入所给的条件求出参数,在第二问,求解的关键是整理成一个二次函数函数值恒正的问题,如此则可以转化为用判别式求解参数的范围,本题训练了转化化归能力
(2)不等式f(x)>2x+m恒成立,即f(x)-2x-m>0恒成立,由判别式求参数即可
解答:解:(1)由题意,设其方程为y=ax2+bx+1代入f(x+1)-f(x)=2x恒成立,整理得2ax+a+b=2x恒成立,既得
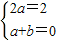 解得
解得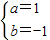
故f(x)=x2-x+1
(2)在R上不等式f(x)>2x+m恒成立,即x2-3x+1-m>0恒成立,故△=9-4(1-m)<0,解得m<-

点评:本题考查函数解析式的求解及常用方法,解题的关键是了解二次函数的解析式的结构利用待定系数法设出解析式,再代入所给的条件求出参数,在第二问,求解的关键是整理成一个二次函数函数值恒正的问题,如此则可以转化为用判别式求解参数的范围,本题训练了转化化归能力

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目