Question

某单位年终联欢活动中，每人参与一次摸奖．摸奖活动规则是：从一个装有大小相同的3个白球和2个红球的袋子中，任意摸出两个球，根据摸出的结果确定奖金额X（元）如下表：

结果	奖金额
两个白球	50
一白球一红球	100
两个红球	200

（1）求X的概率分布表和E（X）；
（2）甲，乙两人分别参加摸奖，求两人获得的奖金额之和不少于300元的概率．

Answer 1

分析：（1）利用排列组合公式，我们易计算出“两个白球”等的个数，及所有事件的总个数，代入古典概型公式，即可得到概率，由于X的可能值为50，100，200，分别计算出X分别取50，100，200时的概率，即可得到X的分布列，代入期望公式，即可得到数学期望EX．
（2）奖金额之和步不小于300，指甲，乙分别获得100，200；200，100；200，200．据此利用X的分布列即可计算出两人获得的奖金额之和不少于300元的概率．

解答：解：（1）因为P（X=50）=

C 2 3

C 2 5

=

3

10

，
P（X=100）=

C 1 2 C 1 3

C 2 5

=

3

5

，
P（X=200）=

C 2 2

C 2 5

=

1

10

，（5分）
所以X的分布列：

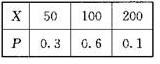
∴E（X）=50×

3

10

+100×

3

5

+200×

1

10

=95．（12分）
（2）奖金额之和小于300，指甲，乙分别获得100，200；200，100；200，200．
概率为0.6×0.1+0.1×0.6+0.1×0.1=0.13
两人获得的奖金额之和不少于300元的概率为0.13．

点评：本题考查的知识点是等可能事件的概率，离散型随机变量及其分布列，散型随机变量的期望与分差，其中在计算X分别取50，100，200时，观察摸球的情况时，要注意不重漏，这是解答本题的易错点．