题目内容
已知函数 的定义域为A,函数
的定义域为A,函数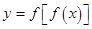 的定义域为B,则( )
的定义域为B,则( )
A.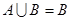 | B.A∈B | C.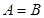 | D.A∩B="B" |
D
解析试题分析:因为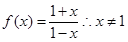 ,则集合A={x|x
,则集合A={x|x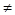 1},而y=f(f(x))的定义域即为f(x)
1},而y=f(f(x))的定义域即为f(x) 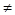 1,且
1,且 得到
得到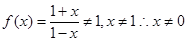 故得到集合B,那么A∩B=B,选D.
故得到集合B,那么A∩B=B,选D.
考点:本题主要考查了函数的定义域的求解的运用。
点评:解决该试题的关键是能利用分式函数得到集合A,同时理解复合函数的定义域的准确理解和表示,进而得到求解。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知集合A={x|x>1},B={x|-1<x<2},则A∪B等于( ).
| A.{x|-1<x<2} | B.{x|x>-1} |
| C.{x|-1<x<1} | D.{x|1<x<2} |
设集合 ,则
,则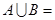 ( )
( )
A.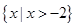 | B.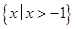 |
C. | D. |
已知全集 ,
, ,则
,则 ( )
( )
A.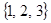 | B. | C. | D.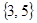 |
方程组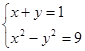 的解集是( )
的解集是( )
A.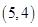 | B.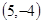 | C.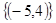 | D.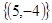 |
已知集合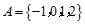 ,
, ,
,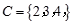 ,则
,则
A.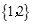 | B. | C. | D. |
已知全集U=R,集合 ,则
,则 等于( )
等于( )
A.{ x ∣0 x x 2} 2} | B.{ x ∣0<x<2} |
| C.{ x ∣x<0或x>2} | D.{ x ∣x 0或x 0或x 2} 2} |
已知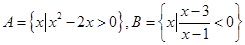 ,则
,则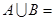 ( )
( )
A.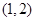 | B.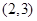 | C. | D.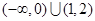 |
设全集是实数集R,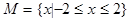 ,
,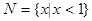 ,则
,则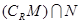 等于( )
等于( )
A.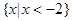 | B.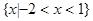 | C.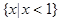 | D.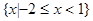 |