题目内容
已知函数
，若实数
是方程
的解，且
，则
的值( )
| A．等于零 | B．恒为负 | C．恒为正 | D．不大于零 |
B
解析试题分析：因为
在
上单调递减，
在
上也单调递减，所以函数在上单调递减，因为
，且，所以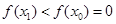
。故B正确。
考点：函数的单调性。
练习册系列答案
阅读快车系列答案
相关题目
若一元二次不等式
对一切实数
都成立，则
的取值范围为（ ）
A． | B． | C． | D． |
若
，则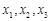
的大小关系为（ ）
A． < < | B．<< | C．<< | D．<< |
设
，
，
，则( )
A． | B． | C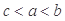． | D． |
函数f(x)=x2+lnx
4的零点所在的区间是（ ）
| A．(0,1) | B．(1,2) | C．(2,3) | D．(3,4) |
设
，则f（6）的值( )
| A．8 | B．7 | C．6 | D．5 |
定义在
上的奇函数
满足：当
时，
，则方程
的实数根的个数是（ ）
| A．1 | B．2 | C．3 | D．5 |
的图象是( )
某厂有许多形状为直角梯形的铁皮边角料,如图,为降低消耗,开源节流,现要从这些边角料上截取矩形铁片(如图中阴影部分)备用,当截取的矩形面积最大时,矩形两边长x,y应为( )
| A．x=15,y=12 | B．x=12,y=15 |
| C．x=14,y=10 | D．x=10,y=14 |