题目内容
记函数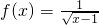 的定义域为A,函数
的定义域为A,函数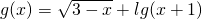 的定义域为B.
的定义域为B.
(1)求A,B;(2)求CR(A∪B)
解:(1)要使函数f(x)有意义,则x-1>0,解得x>1,
即函数的定义域为A=(1,+∞),
由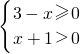 得-1<x≤3,
得-1<x≤3,
即函数g(x)的定义域为B=(-1,3];
(2)由于A∪B=(-1,+∞),
∴CR(A∪B)=(-∞,-1].
分析:(1)根据所给的解析式,利用对数的真数大于零和分母不为零等,列出不等式进行求解,最后要用集合的形式表示.
(2)利用(1)的结论,先求出两个集合的并集,再求CR(A∪B)即得.
点评:本题考查了交、并、补集的混合运算、函数定义域的求法等基本知识.函数定义域即利用对数的真数大于零,分母不为零等等进行求解,注意最后要用集合或区间的形式表示,这是易错的地方.
即函数的定义域为A=(1,+∞),
由
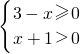 得-1<x≤3,
得-1<x≤3,即函数g(x)的定义域为B=(-1,3];
(2)由于A∪B=(-1,+∞),
∴CR(A∪B)=(-∞,-1].
分析:(1)根据所给的解析式,利用对数的真数大于零和分母不为零等,列出不等式进行求解,最后要用集合的形式表示.
(2)利用(1)的结论,先求出两个集合的并集,再求CR(A∪B)即得.
点评:本题考查了交、并、补集的混合运算、函数定义域的求法等基本知识.函数定义域即利用对数的真数大于零,分母不为零等等进行求解,注意最后要用集合或区间的形式表示,这是易错的地方.

练习册系列答案
相关题目
 的定义域为A,函数
的定义域为A,函数 的定义域为B.
的定义域为B. 的定义域为A,
的定义域为A,
 的定义域为B.
的定义域为B. ,求实数
,求实数 的取值范围.
的取值范围. 的定义域为A,则
的定义域为A,则 中有 个元素。
中有 个元素。 的定义域为A,
的定义域为A, (a < 1)的定义域为B.
(a < 1)的定义域为B. ,求实数a的取值范围.
,求实数a的取值范围.