题目内容
已知关于x的不等式 在x∈(a,+∞)上恒成立,则实数a的最小值为 ( )
在x∈(a,+∞)上恒成立,则实数a的最小值为 ( )
| A.1 |
B. |
| C.2 |
D. |
B
解析

练习册系列答案
相关题目
下列结论正确的是( ).
A.当x>0且x≠1时,lgx+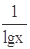 ≥2 ≥2 |
B.当x>0时,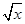 + +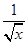 ≥2 ≥2 |
C.x≥2时,x+ 的最小值为2 的最小值为2 |
D.当0<x≤2时,x- 无最大值 无最大值 |
对任意正数x,y不等式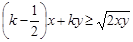 恒成立,则实数
恒成立,则实数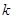 的最小值是 ( )
的最小值是 ( )
| A.1 | B.2 | C.3 | D.4 |
已知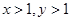 ,且
,且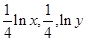 ,成等比数列,则xy( )
,成等比数列,则xy( )
| A.有最大值e | B.有最大值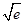 | C.有最小值e | D.有最小值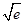 |
设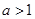 ,
,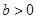 ,若
,若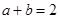 ,则
,则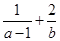 的最小值为( )
的最小值为( )
A.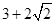 | B.6 | C.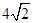 | D.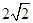 |
已知a>0,b>0,a+b=2,则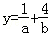 的最小值是( )
的最小值是( )
A.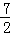 | B.4 | C.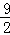 | D.5 |
已知△ABC中,∠C=90°,则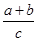 的取值范围是 ( )
的取值范围是 ( )
| A.(0,2) |
B. |
C.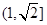 |
D. |
某车间分批生产某种产品,每批的生产准备费用为800元.若每批生产x件,则平均仓储时间为 天,且每件产品每天的仓储费用为1元.为使平均到每件产品的生产准备费用与仓储费用之和最小,每批应生产产品( )
天,且每件产品每天的仓储费用为1元.为使平均到每件产品的生产准备费用与仓储费用之和最小,每批应生产产品( )
| A.60件 | B.80件 |
| C.100件 | D.120件 |
已知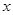 ,
, ,且
,且 ,则
,则 的最大值是( )
的最大值是( )
| A.3 | B.3.5 | C.4 | D.4.5 |