题目内容
设全集U=R,若集合M={y|y= },N={x|y=lg
},N={x|y=lg },则(CUM)∩N=( )
},则(CUM)∩N=( )A.(-3,2)
B.(-3,0)
C.(-∞,1)∪(4,+∞)
D.(-3,1)
【答案】分析:由集合的意义,可得M为函数y=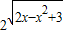 的值域,N为函数y=lg
的值域,N为函数y=lg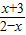 的定义域;对于M,先求t=2x-x2+3的范围,
的定义域;对于M,先求t=2x-x2+3的范围,
再求得0≤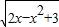 ≤2,进而可得y=
≤2,进而可得y=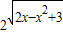 的值域,即可得集合M,由补集的定义可得CUM;对于N,由对数函数的定义域可得集合N,由集合的运算计算可得答案.
的值域,即可得集合M,由补集的定义可得CUM;对于N,由对数函数的定义域可得集合N,由集合的运算计算可得答案.
解答:解:由集合的意义,可得M为函数y=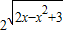 的值域,
的值域,
令t=2x-x2+3,t≥0,
由二次函数的性质可得t=-x2+2x+3=-(x-1)2+4,易得t≤4,
则0≤t≤4,进而可得0≤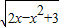 ≤2;
≤2;
在y=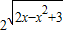 中,有1≤y≤4;
中,有1≤y≤4;
即M={y|1≤y≤4},则(CUM)={y|y<1或y>4};
集合N为函数y=lg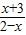 的定义域,则
的定义域,则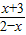 >0,
>0,
解可得-3<x<2,
即N={x|-3<x<2};
则(CUM)∩N={x|-3<x<1}=(-3,1);
故选D.
点评:本题借助集合的运算考查指数函数的值域、对数函数的定义域等有关性质,需要熟练掌握指数函数、对数函数的性质.
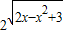 的值域,N为函数y=lg
的值域,N为函数y=lg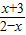 的定义域;对于M,先求t=2x-x2+3的范围,
的定义域;对于M,先求t=2x-x2+3的范围,再求得0≤
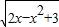 ≤2,进而可得y=
≤2,进而可得y=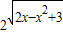 的值域,即可得集合M,由补集的定义可得CUM;对于N,由对数函数的定义域可得集合N,由集合的运算计算可得答案.
的值域,即可得集合M,由补集的定义可得CUM;对于N,由对数函数的定义域可得集合N,由集合的运算计算可得答案.解答:解:由集合的意义,可得M为函数y=
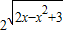 的值域,
的值域,令t=2x-x2+3,t≥0,
由二次函数的性质可得t=-x2+2x+3=-(x-1)2+4,易得t≤4,
则0≤t≤4,进而可得0≤
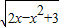 ≤2;
≤2;在y=
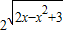 中,有1≤y≤4;
中,有1≤y≤4;即M={y|1≤y≤4},则(CUM)={y|y<1或y>4};
集合N为函数y=lg
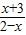 的定义域,则
的定义域,则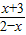 >0,
>0,解可得-3<x<2,
即N={x|-3<x<2};
则(CUM)∩N={x|-3<x<1}=(-3,1);
故选D.
点评:本题借助集合的运算考查指数函数的值域、对数函数的定义域等有关性质,需要熟练掌握指数函数、对数函数的性质.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
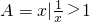 ,则?UA=________.
,则?UA=________. },N={x|y=lg
},N={x|y=lg },则(CUM)∩N=( )
},则(CUM)∩N=( )