题目内容
已知幂函数f(x)=xm2-2m-3(m∈Z)的图象与x轴、y轴无公共点且关于y轴对称.
(1)求m的值;
(2)画出函数y=f(x)的图象(图象上要反映出描点的“痕迹”).
(1)求m的值;
(2)画出函数y=f(x)的图象(图象上要反映出描点的“痕迹”).
分析:(1)幂函数f(x)=xm2-2m-3(m∈Z)的图象与x,y轴都无公共点说明指数为负数,而图形关于y轴对称说明指数数为偶函数,由此求得整数m的值.
(2)根据(1)中结论写出幂函数的解析式,画出函数y=f(x)的图象.
(2)根据(1)中结论写出幂函数的解析式,画出函数y=f(x)的图象.
解答: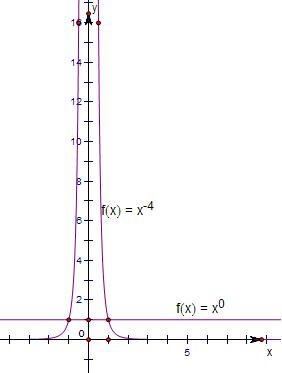 解:(1)由于幂函数f(x)=xm2-2m-3(m∈Z)的图象与x轴、y轴都无公共点,且关于y轴对称,故幂函数是偶函数,
解:(1)由于幂函数f(x)=xm2-2m-3(m∈Z)的图象与x轴、y轴都无公共点,且关于y轴对称,故幂函数是偶函数,
且m2-2m-3=(m-3)(m+1)为非正的偶数.
由m2-2m-3≤0可得-1≤m≤3,即 m=-1、0、1、2,3.
再由m2-2m-3为偶数,可得m=-1、1、3.
(2)当m=-1或3时,f(x)=x0;
当m=1时,f(x)=x-4;
图象如图所示.
 解:(1)由于幂函数f(x)=xm2-2m-3(m∈Z)的图象与x轴、y轴都无公共点,且关于y轴对称,故幂函数是偶函数,
解:(1)由于幂函数f(x)=xm2-2m-3(m∈Z)的图象与x轴、y轴都无公共点,且关于y轴对称,故幂函数是偶函数,且m2-2m-3=(m-3)(m+1)为非正的偶数.
由m2-2m-3≤0可得-1≤m≤3,即 m=-1、0、1、2,3.
再由m2-2m-3为偶数,可得m=-1、1、3.
(2)当m=-1或3时,f(x)=x0;
当m=1时,f(x)=x-4;
图象如图所示.
点评:此题很好的考查了幂函数的图象与性质,属于基础题.

练习册系列答案
相关题目