题目内容
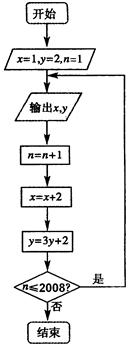
(12分)根据如图所示的程序框图,将输出的x、y值依次分别记为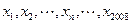 ;
;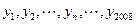
(Ⅰ)求数列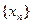 的通项公式
的通项公式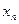 ;
;
(Ⅱ)写出y1,y2,y3,y4,由此猜想出数列{yn}的一个通项公式yn,并证明你的结论;
(Ⅲ)求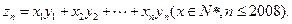
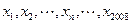 ;
;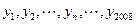
(Ⅰ)求数列
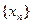 的通项公式
的通项公式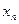 ;
;(Ⅱ)写出y1,y2,y3,y4,由此猜想出数列{yn}的一个通项公式yn,并证明你的结论;
(Ⅲ)求
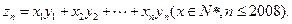

(Ⅰ)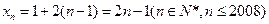
(Ⅱ)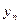 =3n-1(
=3n-1( ) ,证明略
) ,证明略
(Ⅲ)略
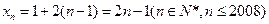
(Ⅱ)
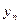 =3n-1(
=3n-1( ) ,证明略
) ,证明略(Ⅲ)略
解:(Ⅰ)由框图,知数列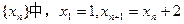 ………2分
………2分
∴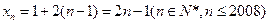 ………4分
………4分
(Ⅱ)由框图,知数列{yn}中,yn+1=3yn+2 ………5分
∴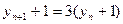 ………6分
………6分
∴ ∴数列{yn+1}是
∴数列{yn+1}是 以3为首项,3为公比的等比数列。
以3为首项,3为公比的等比数列。
∴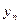 +1=3·3n-1=3n
+1=3·3n-1=3n
∴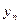 =3n-1(
=3n-1( ) ………8分
) ………8分
(Ⅲ)zn=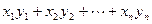
=1×(3-1)+3×(32-1)+…+(2n-1)(3n-1)
=1×3+3×32+…+(2n-1)·3n-[1+3+…+(2n-1)] ………9分
记Sn=1×3+3×32+…+(2n-1)·3n,①
则3Sn=1×32+3×33+…+(2n-1)×3n+1 ②
①-②,得-2Sn=3+2·32+2·33+…+2·3n-(2n-1)·3n+1
=2(3+32+…+3n)-3-(2n-1)·3n+1
=2×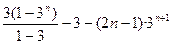 =
=
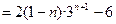
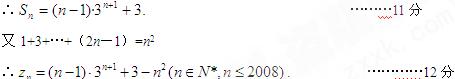
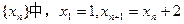 ………2分
………2分∴
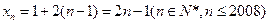 ………4分
………4分(Ⅱ)由框图,知数列{yn}中,yn+1=3yn+2 ………5分
∴
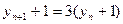 ………6分
………6分∴
 ∴数列{yn+1}是
∴数列{yn+1}是 以3为首项,3为公比的等比数列。
以3为首项,3为公比的等比数列。 ∴
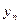 +1=3·3n-1=3n
+1=3·3n-1=3n∴
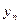 =3n-1(
=3n-1( ) ………8分
) ………8分(Ⅲ)zn=
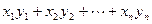
=1×(3-1)+3×(32-1)+…+(2n-1)(3n-1)
=1×3+3×32+…+(2n-1)·3n-[1+3+…+(2n-1)] ………9分
记Sn=1×3+3×32+…+(2n-1)·3n,①
则3Sn=1×32+3×33+…+(2n-1)×3n+1 ②
①-②,得-2Sn=3+2·32+2·33+…+2·3n-(2n-1)·3n+1
=2(3+32+…+3n)-3-(2n-1)·3n+1
=2×
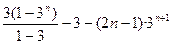 =
=
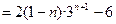
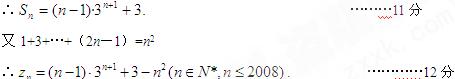

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 ,则输出的
,则输出的 .
. 
 值的一个流程图
值的一个流程图 ,那么判断框中应填入的关于
,那么判断框中应填入的关于 的条件是( )
的条件是( )




 程序框图。
程序框图。






