题目内容
已知点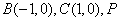 是平面上一动点,且满足
是平面上一动点,且满足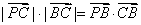
(1)求点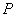 的轨迹C对应的方程;
的轨迹C对应的方程;
(2)已知点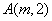 在曲线C上,过点A作曲线C的两条弦
在曲线C上,过点A作曲线C的两条弦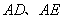 ,且
,且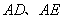 的斜率
的斜率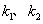 =2试推断:动直线
=2试推断:动直线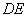 是否过定点?证明你的结论。
是否过定点?证明你的结论。
【答案】
解:(1)设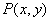 代入
代入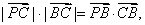 得
得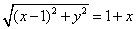
化简得
(2)将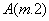 代入
代入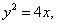 得
得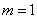 ,
,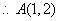
法一: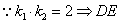 两点不可能关于
两点不可能关于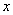 轴对称,
轴对称,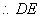 的斜率必存在
的斜率必存在
设直线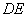 的方程
的方程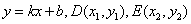
由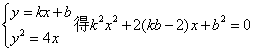

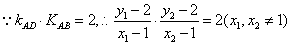 7分
7分
且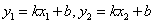
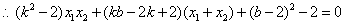 8分
8分
将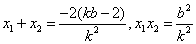 代入化简
代入化简
将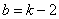 代入
代入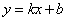 得
得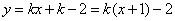 ,过定点(-1.-2)
,过定点(-1.-2)
将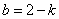 入
入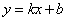 得
得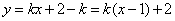 ,过定点(1,2)即为A点,舍去
,过定点(1,2)即为A点,舍去
 直线
直线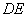 过定点为(-1,-2)
过定点为(-1,-2)
法二:设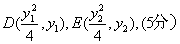 则
则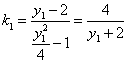
同理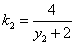 ,由已知得
,由已知得
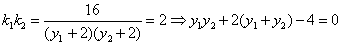
设直线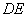 的方程为
的方程为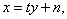 代入
代入
得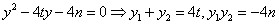
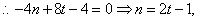 直线
直线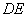 的方程为
的方程为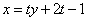
即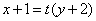 直线
直线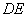 过定点(-1,-2)
过定点(-1,-2)

练习册系列答案
相关题目
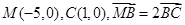 ,
,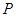 是平面上一动点,且满足
是平面上一动点,且满足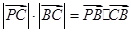 ,
,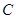 对应的方程;
对应的方程;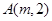 在曲线
在曲线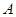 作曲线
作曲线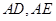 ,且
,且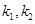 满足
满足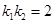 ,试判断动直线
,试判断动直线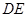 是否过定点,并证明你的结论.
是否过定点,并证明你的结论.