题目内容
已知变量x,y满足约束条件
,则目标函数z=x+y的最大值为
|
3
3
.分析:画出满足约束条件的可行域,并求出各角点的坐标,代入目标函数的解析式,分别求出对应的函数值,比较后可得答案.
解答:解:满足约束条件
的可行域如下图所示,
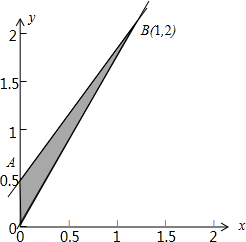
∵目标函数z=x+y
∴zO=0+0=0,
zA=0+0.5=0.5,
zB=1+2=3,
故目标函数z=x+y的最大值为3
故答案为:3
|

∵目标函数z=x+y
∴zO=0+0=0,
zA=0+0.5=0.5,
zB=1+2=3,
故目标函数z=x+y的最大值为3
故答案为:3
点评:本题考查的知识点是简单线性规划,角点法是解答此类问题最常用的方法,常用来求解选择和填空题.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
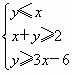 ,则目标函数Z=2x+y的最大值为________.
,则目标函数Z=2x+y的最大值为________. 则目标函数
则目标函数