题目内容
已知R为全集,不等式2x≥| 1 |
| 2 |
| 1-log2x |
分析:(1)先根据不等式2x≥
?2x≥2-1?x≥-1求出集合A;再根据1-log2x≥0以及真数大于0求出B;
(2)先求出B的补集,再结合所求出的集合A即可得到A∩CRB.
| 1 |
| 2 |
(2)先求出B的补集,再结合所求出的集合A即可得到A∩CRB.
解答:解:(1)不等式2x≥
?2x≥2-1?x≥-1.
故A={x|x≥-1}.
因为函数y=
中1-log2x≥0?log2x≤1=log22?0<x≤2.
故B={x|0<x≤2}.
(2)根据上面的结论得:CRB={x|x≤0,x>2}.
所以:A∩CRB={x|-1≤x≤0,x>2}.
| 1 |
| 2 |
故A={x|x≥-1}.
因为函数y=
| 1-log2x |
故B={x|0<x≤2}.
(2)根据上面的结论得:CRB={x|x≤0,x>2}.
所以:A∩CRB={x|-1≤x≤0,x>2}.
点评:本题主要考查集合的基本运算以及对数函数的定义域的求法.在求对数函数的定义域时,一定要注意真数大于0这一限制条件,避免出错.

练习册系列答案
相关题目
 的解集为A,函数
的解集为A,函数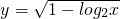 的定义域为B,求:(1)集合A与集合B;(2)求A∩CRB.
的定义域为B,求:(1)集合A与集合B;(2)求A∩CRB.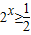 的解集为A,函数
的解集为A,函数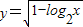 的定义域为B,求:(1)集合A与集合B;(2)求A∩CRB.
的定义域为B,求:(1)集合A与集合B;(2)求A∩CRB.