Question

设不等式组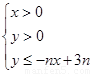所表示的平面区域为D_n，记D_n内 的整点个数为a_n(n∈N^*)(整点即横坐标和纵坐标均为整数的点)．

(1) 求证：数列{a_n}的通项公式是a_n＝3n(n∈N^*)．

(2) 记数列{a_n}的前n项和为S_n，且T_n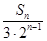＝．若对于一切的正整数n，总有T_n≤m，求实数m的取值范围．

 

Answer 1

【答案】

(1)详见试题解析；(2)．

【解析】

试题分析：(1)首先由已知，得，，或，内的整点在直线和上．记直线为，与直线和的交点的纵坐标分别为，则可求得的值，最后可得的表达式；(2)由(1)先求出及的表达式，由已知对一切的正整数，恒成立，等价于，可以利用数列相邻两项的差，解，得到数列的最大项，从而可得实数的取值范围．

试题解析：(1)证明：由，得，，或，内的整点在直线和上．记直线为，与直线和的交点的纵坐标分别为，则，．

(2)，，，∴当时，，且，于是，是数列中的最大项，故．

考点：1．线性规划整点问题；2．数列通项公式及前项和的求法；3．恒成立不等式中的参数取值范围问题．