题目内容
对于R上可导的任意函数 ,若满足
,若满足 ,则必有 ( )
,则必有 ( )
A. | B. |
C. | D. |
C
解析试题分析:因为 ,所以,1-x≥0即x≤1时,
,所以,1-x≥0即x≤1时, <0, 1-x≤0即x≥1时,
<0, 1-x≤0即x≥1时, >0,即函数
>0,即函数 在 [1,+∞)上的单调增,在(-∞,1)上单调递减,所以f(0)>f(1),f(2)>f(1) f(0)+f(2)>2f(1) 所以f(0)+f(2)>="2f(1)" ,故选C.
在 [1,+∞)上的单调增,在(-∞,1)上单调递减,所以f(0)>f(1),f(2)>f(1) f(0)+f(2)>2f(1) 所以f(0)+f(2)>="2f(1)" ,故选C.
考点:函数导数的性质

练习册系列答案
相关题目
若函数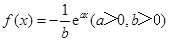 的图象在
的图象在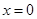 处的切线与圆
处的切线与圆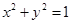 相切,则
相切,则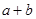 的最大值是( )
的最大值是( )
| A.4 | B.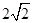 | C.2 | D.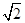 |
设函数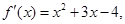 则
则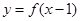 的单调减区间( )
的单调减区间( )
A.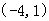 | B.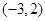 | C.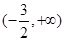 | D.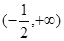 |
定义在R上的函数f(x)满足f(4)=1,f′(x)为函数f(x)的导函数.已知函数y=f′(x)的图象如图所示,两个正数a、b满足f(2a+b)<1,则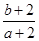 的取值范围是( )
的取值范围是( )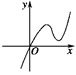
A.(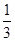 , ,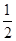 ) ) | B.(-∞,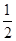 )∪(3,+∞) )∪(3,+∞) | C.(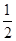 ,3) ,3) | D.(-∞,-3) |
由直线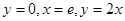 及曲线
及曲线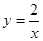 所围成的封闭的图形的面积为( )
所围成的封闭的图形的面积为( )
A.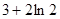 | B.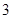 | C.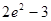 | D. |
若曲线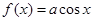 与曲线
与曲线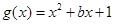 在交点
在交点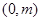 处有公切线, 则
处有公切线, 则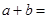 ( )
( )
A. | B. | C.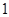 | D.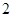 |
函数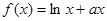 存在与直线
存在与直线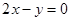 平行的切线,则实数
平行的切线,则实数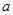 的取值范围是( )
的取值范围是( )
A.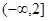 | B.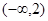 | C. | D. |
已知函数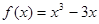 ,若过点
,若过点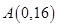 且与曲线
且与曲线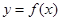 相切的切线方程为
相切的切线方程为 ,则实数
,则实数 的值是( )
的值是( )
A. | B.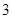 | C.6 | D.9 |
已知函数f(x)= ,若| f(x)|≥ax,则a的取值范围是( )
,若| f(x)|≥ax,则a的取值范围是( )
| A.(-∞,0] | B.(-∞,1] | C.[-2,1] | D.[-2,0] |