题目内容
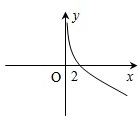定义在（-∞，0）∪（0，+∞）上的奇函数f（x）在（0，+∞）上是减函数，且在x＞0时，f（x）的图象如图所示，则不等式x[f（x）-f（-x）]＞0的解集为（ ）| A、（-∞，-2）∪（0，2） | B、（-∞，-2）∪（2，+∞） | C、（-2，0）∪（2，+∞） | D、（-2，0）∪（0，2） |
分析：由函数f（x）是定义在R上的奇函数，f（2）=0，则f（-2）=0，由于f（x）在（0，+∞）上是减函数，所以f（x）在（-∞，0）上是减函数，从而可得不等式组，故可得答案．
解答：解：由于函数为奇函数，所以不等式可化为xf（x）＞0，∴
或
∵f（x）在（0，+∞）上是减函数，∴f（x）在（-∞，0）上是减函数
∵f（2）=0，∴f（-2）=0
∴
或
∴x∈（-2，0）∪（0，2）
故选D．
|
|
∵f（x）在（0，+∞）上是减函数，∴f（x）在（-∞，0）上是减函数
∵f（2）=0，∴f（-2）=0
∴
|
|
∴x∈（-2，0）∪（0，2）
故选D．
点评：解答本题的关键是根据已知条件，结合奇函数的性质，找出函数的零点，并以零点为端点将定义域分为几个不同的区间，然后在每个区间上结合函数的单调性进行讨论，这是分类讨论思想在解决问题的巨大作用的最好体现，分类讨论思想往往能将一个复杂的问题的简单化，是高中阶段必须要掌握的一种方法．
练习册系列答案
相关题目
若定义在（-1，0）内的函数f（x）=log2a（x+1）＞0，则a的取值范围是（ ）
A、(0，
| ||
B、(0，
| ||
C、(
| ||
| D、（0，+∞） |