题目内容
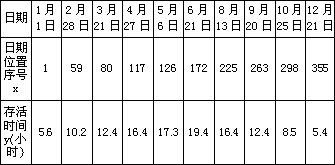
在自然条件下,一年中10次测量的某种细菌一天内存活时间的统计表(时间近似到0.1小时)如下表所示:
| 日期 | 1月 1日 | 2月 28日 | 3月 21日 | 4月 27日 | 5月 27日 | 6月 21日 | 8月 13日 | 9月 20日 | 10月 25日 | 12月 21日 |
| 日期位置序号x | 1 | 59 | 80 | 117 | 126 | 172 | 225 | 263 | 298 | 355 |
| 存活时间y(小时) | 5.6 | 10.2 | 12.3 | 16.4 | 17.3 | 19.4 | 16.4 | 12.5 | 8.5 | 5.4 |
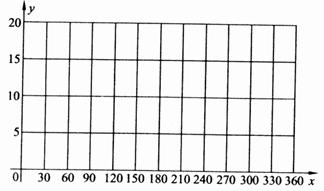
(1) 以日期在365天中的位置序号为横坐标,一天内存活时间为纵坐标,在给定坐标系中画出这些数据的散点图.
(2) 试选用一个形如![]() +t的函数来近似描述一年中该细菌一天内的存活时间y与日期位置序号x之间的函数关系.(注:①求出所选用的函数关系式;②一年按365天计算)
+t的函数来近似描述一年中该细菌一天内的存活时间y与日期位置序号x之间的函数关系.(注:①求出所选用的函数关系式;②一年按365天计算)
(3) 用(2)中的函数模型估计该种细菌一年中大约有多少天的存活时间大于15.9小时.
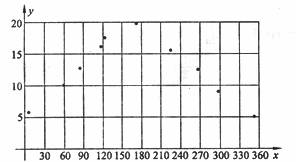
解:(1)散点图为:
(2)由散点图知细菌存活时间与日期序号之间的函数关系近似为![]() ,由图形知函数的最大值为19.4,最小值为5.4,即,
,由图形知函数的最大值为19.4,最小值为5.4,即,![]()
由19.4-5.4=14得A=7;由19.4+5.4=24.8得t=12.4;又T=365,![]() ,
,
当x=172时,![]()
![]()
(3)由y>15.9得![]() ,
,
![]() 解得112
解得112![]() x
x![]() 232
232
答该种细菌大约有121天(或122天)中存活时间大于15.9小时

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目