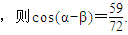题目内容
现知结论,请在横线上填写原题的一个条件,已知α,β均锐角,且sinα-sinβ=-
,
.
| 1 |
| 2 |
cosα+cosβ=
| ||
| 3 |
cosα+cosβ=
,则cos(α-β)=
| ||
| 3 |
| 59 |
| 72 |
分析:观察条件和结论发现条件缺少cosαcosβ,故可构造cosα+cosβ=t,利用待定系数法求出t即可.
解答:解:∵sinα-sinβ=-
∴(sinα-sinβ)2=1-2sinαsinβ=
解得sinαsinβ=
设cosα+cosβ=t t>0
(cosα+cosβ)2=1+2cosαcosβ=t2
解得cosαcosβ=
而cos(α-β)=cosαcosβ+sinαsinβ=
+
=
解得:t=
故答案为cosα+cosβ=
| 1 |
| 2 |
∴(sinα-sinβ)2=1-2sinαsinβ=
| 1 |
| 4 |
解得sinαsinβ=
| 3 |
| 8 |
设cosα+cosβ=t t>0
(cosα+cosβ)2=1+2cosαcosβ=t2
解得cosαcosβ=
| t2-1 |
| 2 |
而cos(α-β)=cosαcosβ+sinαsinβ=
| t2-1 |
| 2 |
| 3 |
| 8 |
| 59 |
| 72 |
解得:t=
| ||
| 3 |
故答案为cosα+cosβ=
| ||
| 3 |
点评:本题主要考查了运用诱导公式化简求值,以及两角和与差的余弦函数,属于基础题.

练习册系列答案
相关题目
 ,则
,则 ..
.. ,
,