题目内容
(满分14分)已知二次函数f(x)的二次项系数为a,且不等式f(x)>-2x的解集为(1,3).
(1)若方程f(x)+6a=0有两个相等的根,求f(x)的解析式;
(2)若f(x)的最大值为正数,求实数a的取值范围.
解:本题主要考查二次函数、方程的根与系数关系,考查运用数学知识解决问题的能力.
(1)∵f(x)+2x>0的解集为(1,3).
∴f(x)+2x=a(x-1)(x-3),且a<0,因而
f(x)=a(x-1)(x-3)-2x=ax2-(2+4a)x+3a. ①
由方程f(x)+6a=0,得ax2-(2+4a)x+9a=0.②
∵方程②有两个相等的根,∴Δ=[-(2+4a)]2-4a·9a=0,即5a2-4a-1=0.
解得a=1或a=-. 由于a<0,舍去a=1,将a=-代入①得
f(x)的解析式为f(x)=-x2-x-.
(2)由f(x)=ax2-2(1+2a)x+3a=a2-
及a<0,可得f(x)的最大值为-. 由
解得a<-2-或-2+<a<0.
故当f(x)的最大值为正数时,实数a的取值范围是(-∞,-2-)∪(-2+,0).
解析

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
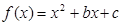 的图象过点
的图象过点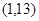 ,且函数对称轴方程为
,且函数对称轴方程为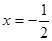 .
.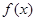 的解析式;
的解析式;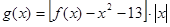 ,求
,求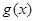 在区间
在区间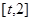 上的最小值
上的最小值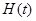 ;
;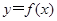 的图象上是否存在这样的点,使它的横坐标是正整数,纵坐标是一个完全平方数?如果存在,求出这样的点的坐标;如果不存在,请说明理由.
的图象上是否存在这样的点,使它的横坐标是正整数,纵坐标是一个完全平方数?如果存在,求出这样的点的坐标;如果不存在,请说明理由. (
( )的导函数
)的导函数 的解析式;
的解析式; ,求
,求 在
在 上的最大值.
上的最大值.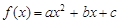 满足:①
满足:①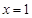 时有极值;②图象过点
时有极值;②图象过点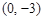 ,且在该点处的切线斜率为
,且在该点处的切线斜率为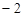 .
.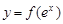 上任意一点的切线的斜率恒大于
上任意一点的切线的斜率恒大于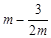 ,求
,求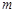 的取值范围;
的取值范围;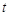 满足什么条件时,函数
满足什么条件时,函数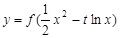 的图象与坐标轴没有公共点?
的图象与坐标轴没有公共点?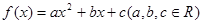 ,且同时满足下列条件:
,且同时满足下列条件: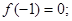 ② 对任意的实数
② 对任意的实数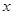 ,都有
,都有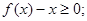
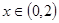 时,有
时,有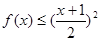 。
。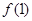 ;
;
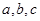 的值;
的值;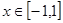 时,函数
时,函数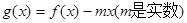 是单调函数,求
是单调函数,求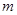 的取值范围。
的取值范围。